Равновесная химическая термодинамика. Основы классической термодинамики. Термодинамическое описание химических процессов, страница 9

Так как для регулярных растворов изменение объема и энтропии при смешении не происходит, то

Итак,

                                                                         (8.17)

Зная , можно найти  и  :

 ,                                                                                            (8.18)

Для активности и коэффициентов активности обоих компонентов получаем:

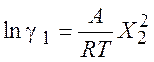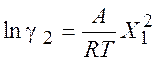 ,                                                                                (8.19)

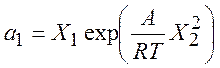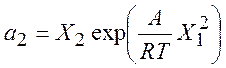 ,                                                         (8.20)

Энергия Гиббса смешения равна

                                                                                  (8.21)

8.5. Осмотическое давление

Явление осмоса заключается в диффузии молекул растворителя через полупроницаемую мембрану, пропускающую только растворитель и разделяющую чистый растворитель  и раствор (или растворы с различной концентрацией).

Химический потенциал растворителя в растворе равен

Если раствор близок к идеальному и мольная доля растворенного вещества , то

                                                         (8.22)

Теперь можно поставить вопрос: какое давление P следует приложить к раствору, чтобы химический потенциал растворителя в растворе стал равен химическому потенциалу чистого растворителя?  Изменение  под давлением

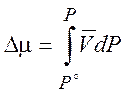                                                                                                                 (8.23)

где  - парциальный мольный объем растворителя. Считая, что  не зависит от P, получаем

                                                                                                  (8.24)

где  - осмотическое давление. Уравнивая выражения (8.22) и (8.24), находим

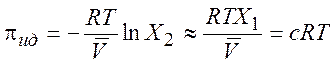                                                                              (8.25)

8.6. Химическое равновесие

Пусть в системе протекает химическая реакция

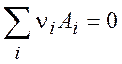
Тогда, в соответствии с общим условием равновесия

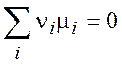
константа равновесия выражается через активности компонентов:

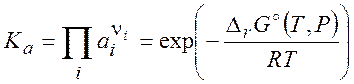                                                                           (8.26)

Глава 9. Термодинамика растворов электролитов

9.1. Формула Борна для энергии сольватации

Электролит – вещество, молекулы которого в растворе способны распадаться на ионы. Сольватация – процесс перехода иона из вакуума в раствор. Энергия сольватации – изменение энергии Гиббса в процессе сольватации.

Энергия образования иона в вакууме:

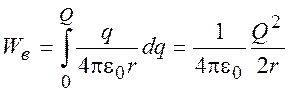                                                                                        (9.1)

Энергия образования иона в растворе:

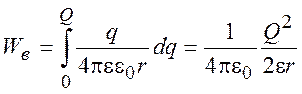                                                                                      (9.2)

Следовательно, энергия сольватации

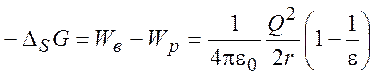                                                                          (9.3)

9.2. Уравнение Пуассона

Описание термодинамических свойств ионов в растворах через активность и коэффициенты активности осуществляется в рамках теории Дебая-Хюккеля. В самом простейшем варианте теории будем считать все ионы точечными.

Вычислим электростатический потенциал отдельного иона в зависимости от расстояния от его центра. Для нахождения усредненного потенциала необходимо решить сферически симметричное уравнение Пуассона:

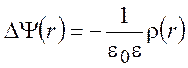                                                                                                         (9.4)

где  -оператор Лапласа;  - электростатический потенциал;  - плонтость зарядов на расстоянии r от центрального иона. На расстоянии rот рассматриваемого иона концентрации положительных  и отрицательных  ионов изменяются в соответствии с законом Больцмана:

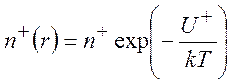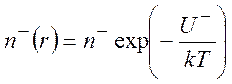 ,                                                                    (9.5)

где

 ,                                                                                  (9.6)

Z – абсолютное значение заряда иона в единицах заряда электрона; n⁺ и n^- - средние концентрации анионов и катионов. Если в растворе присутствуют ионы с разными зарядами, то для  получаем