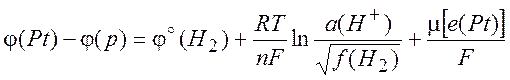Равновесная химическая термодинамика. Основы классической термодинамики. Термодинамическое описание химических процессов, страница 13

                                                 (10.2)

где

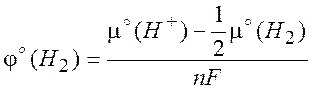                                                                                  (10.3)

представляет собой стандартный электродный потенциал водородного электрода, принимаемый равным нулю для указанных выше стандартных условий. Величину

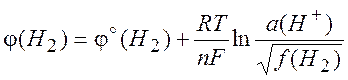                                                                            (10.4)

называют потенциалом полуэлемента, или электродным потенциалом. Эту величину записывают в общем виде

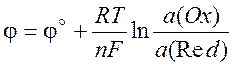                                                                                               (10.5)

10.3. Напряжение гальванического элемента

Гальванический элемент – два электрода, соединенные проводником. Напряжение гальванического элемента – это предельное значение разности электродных потенциалов, при токе через элемент, стремящемся к нулю.

Например, гальванический элемент из двух электродов первого рода:

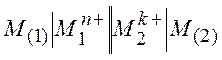
Исходя из общей формулы (10.5), запишем выражения для потенциалов обоих электродов:

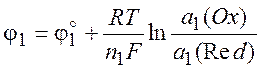
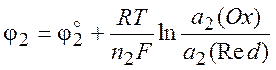
Напряжение гальванического элемента:

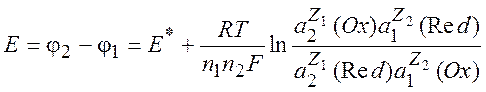                                                     (10.6)

где

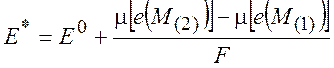                                                                              (10.7)

Величину E⁰ называют стандартной разностью электродных потенциалов:

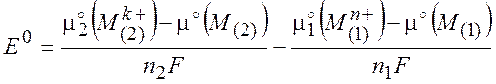                                                   (10.8)

Уравнение (10.6) называется уравнением Нернста.

10.4. Распределение и потоки ионов через мембрану

Движение ионов через полупроницаемую мембрану может привести к возникновению разности электрических потенциалов на мембране, из за разной проницаемости мембраны для разных ионов. Эта разность потенциалов влияет на равновесное распределение других ионов, переносимых через мембрану.

Рассмотрим раствор, содержащий ионы X⁺ и Y ^-, разделенный мембраной на две части (1) и (2), каждая из которых характеризуется концентрациями ионов и своим электрическим потенциалом: (,, ) и (,,). Выпишем выражения для химического потенциала катиона в первой и во второй части системы:

                                                                         (10.9)

                                                                       (10.10)

В равновесии выполняется равенство химических потенциалов:

 

откуда следует, что

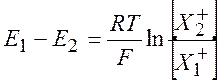                                                                                               (10.11)

Аналогично, для аниона :

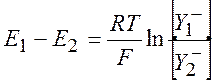                                                                                              (10.12)

Сравнивая уравнения (10.11) и (10.12), получаем

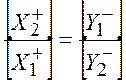                    (Доннаново равновесие)                                                 (10.13)

Глава 11. Адсорбция

11.1. Поверхностная адсорбция

Физическая адсорбция – происходит за счет дисперсионных (ван-дер-ваальсовых) взаимодействий молекул, образования водородных связей и других сил электростатического характера. Характерная теплота адсорбции 2-5 кДж/моль.

Химическая адсорбция – происходит за счет образования химических связей. Характерная теплота адсорбции 10 кДж/моль.Может сопровождаться диссоциацией молекул адсорбата и другими его химическими превращениями.

11.2. Изотерма адсорбции Ленгмюра

Рассмотрим процесс адсорбции с учетом степени заполнения монослоя на поверхности:

Если N_п- полное число мест на поверхности, и  - степень заполнения поверхности, то константа равновесия равна

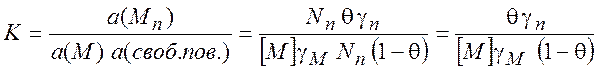                                  (11.1)

где  - концентрация адсорбата (вещества M) в среде,  - коэффициент активности адсорбата в среде,   - коэффициент активности поверхностных молекул. Уравнение (11.1) можно преобразовать к виду

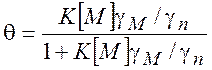                  (изотерма Ленгмюра)                                          (11.2)