Равновесная химическая термодинамика. Основы классической термодинамики. Термодинамическое описание химических процессов, страница 2

Мерой числа способов () реализации состояния системы  является энтропия:

                                                                       (1.15)

где =1.380662 10^-23 Дж/К (постоянная Больцмана). Так как число способов реализации состояния системы не зависит от пути перехода в это состояние, то энтропия является функцией состояния системы.

Для закрытых систем:

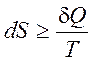                                                                                                                      (1.16)

Выражение (1.16) является математической формулировкой второго начала термодинамики.

Для обратимых процессов:

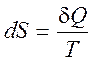                                                                                                                      (1.17)

При T= 0 существует только один способ реализации состояния системы (третье начало термодинамики):

                                                                                                                    (1.18)

Выражая  из (1.16) и подставляя в (1.7) получаем основное термодинамическое равенство:

                                                                                                                     (1.19)

1.4. Термодинамические потенциалы

Внутренняя энергия  является термодинамическим потенциалом (изохорно-изоэнтропийный потенциал). Естественными переменными для внутренней энергии  являются  и . Другие термодинамические потенциалы:

 - энтальпия (теплосодержание), изобарно-изоэнтропийный потенциал;

 - свободная энергия (энергия Гельмгольца), изохорно-изотермический потенциал;

 - энергия Гиббса, изобарно-изотермический потенциал.

Для дифференциалов этих функций:

                                                                                                          (1.20)

                                                                                                       (1.21)

                                                                                                        (1.22)

1.5. Термодинамические соотношения между величинами

Из равенств (1.19) - (1.22) можно получить следующие термодинамические соотношения (соотношения Максвелла)

 ,      ,            ,

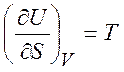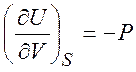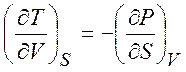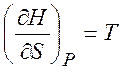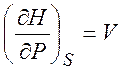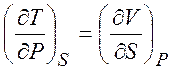 ,      ,              ,                                       (1.23)

 ,     ,             ,

 ,     ,               ,

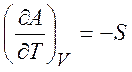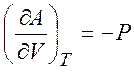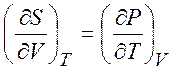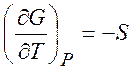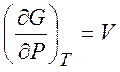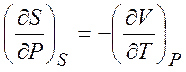и выражения для теплоемкостей

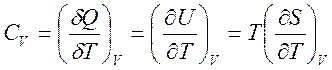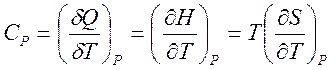,            ,           (1.24)

и уравнения Гиббса-Гельмгольца

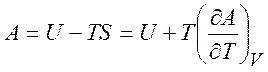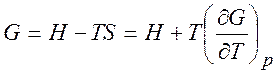,              .                                  (1.25)

Термодинамические соотношения можно получать также путем замены переменных, используя якобианы:

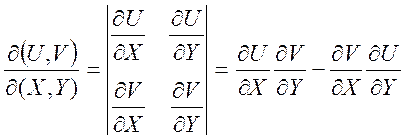                                                                  (1.26)

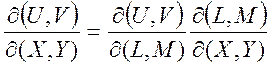                                                                                         (1.27)

Можно показать, что:

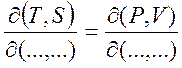                                                                                                        (1.28)

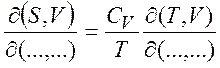                                                                                                 (1.29)

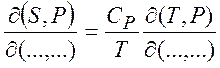                                                                                                 (1.30)

Пример:

 

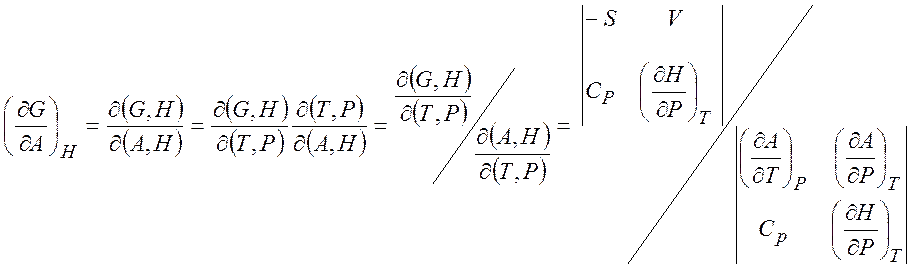
1.6. Химический потенциал

Рассмотрим термодинамическую систему с переменным числом частиц :

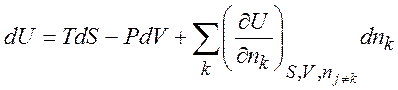                                                                    (1.31)

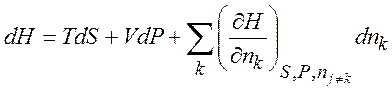                                                                     (1.32)

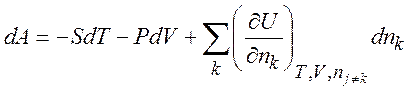                                                                  (1.33)

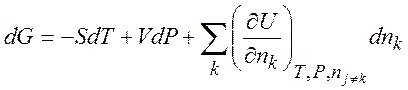                                                                  (1.34)

Исходя из определения dH, dAи dG , получаем:

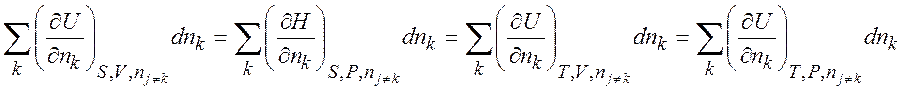
откуда следует, что

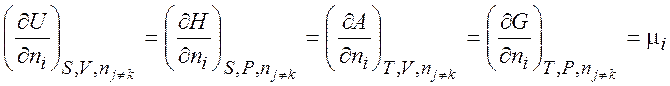      (хим. потенциал)

итак,

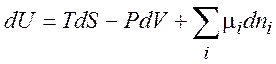                                                                                        (1.35)

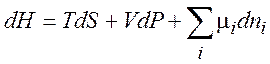                                                                                         (1.36)

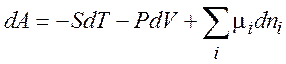                                                                                      (1.37)