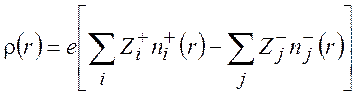Равновесная химическая термодинамика. Основы классической термодинамики. Термодинамическое описание химических процессов, страница 10

                                                                            (9.7)

Используя уравнения (9.5) и (9.6), получаем

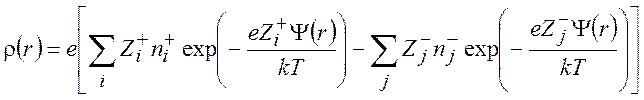                             (9.8)

Разлагая экспоненты в выражении (9.8) в ряд и ограничиваясь в каждом разложении двумя слагаемыми, а также учитывая электронейтральность раствора

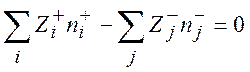                                                                                              (9.9)

получаем

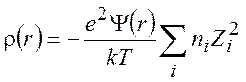                                                                                             (9.10)

где суммирование распространено на все катионы и анионы, присутствующие в растворе. Подставляя (9.10) в (9.4), находим

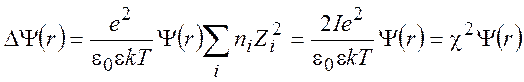                                               (9.11)

Величина I называется ионной силой раствора:

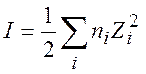                                                                                                              (9.12)                

9.2. Решение уравнения Пуассона

Уравнение Пуассона (9.11) называется уравнением Дебая-Хюккеля. В случае сферической симметрии это уравнение принимает вид:

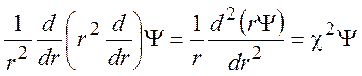                                                                          (9.13)

Решение этого уравнения известно:

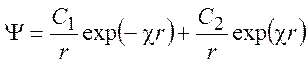                                                                                   (9.14)

 при , поэтому C₂ = 0. Постоянную C₁ можно найти из условия, что при  величина  стремится к потенциалу точечного заряда. Тогда

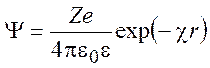                                                                                                   (9.15)

Величину  называют радиусом ионной атмосферы.

9.2. Коэффициент активности ионов

Коэффициент активности ионов рассчитаем, зная разность химических потенциалов реального и идеального растворов:

 

Разность  равна работе по отключению взаимодействий. Величина межионного взаимодействия определяется энергией взаимодействия со своей ионной атмосферой. Для расчета энергии этого взаимодействия найдем электростатический потенциал , который создается только за счет ионной атмосферы:

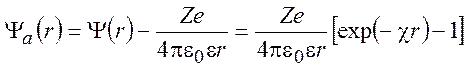                                                        (9.16)

Потенциал, создаваемый ионной атмосферой в центре координат:

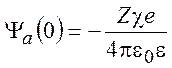
В процессе включения межионных взаимодействий энергия взаимодействия определяется выражением:

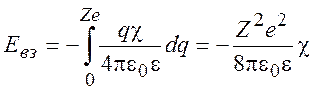                                                                                  (9.17)

Мольная энергия взаимодействия равна

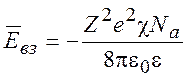                                                                                                       (9.18)

Следовательно,

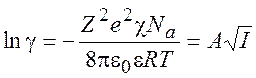                                                                                           (9.19)

9.3. Теория Дебая-Хюккеля во втором приближении

Теория Дебая-Хюкеля  позволяет учитывать конечные размеры ионов. Пусть ион представляет собой сферу радиусом a. Решение Пуассона сохраняется:

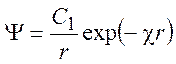
Величину константы C₁ будем определять из условия, что напряженность электрического поля на границе ион-раствор не зависит от способа вычисления:

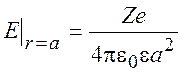
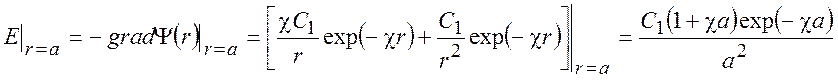
В результате получаем:

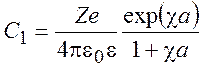                                                                                                    (9.20)

Повторяя предыдущие рассуждения, для  находим

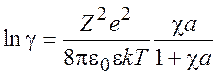                                                                                                  (9.21)

9.3. Среднеионный коэффициент активности

В растворах электролитов невозможно изменять концентрацию только катионов, не меняя при этом концентрацию анионов. Поэтому экспериментальные данные позволяют определить только среднеионный коэффициент активности.

Рассмотрим электролит типа M_mL_l, диссоциирующий на ионы по уравнению

                                                                                            (9.22)

Энергия Гиббса исходной соли, растворенной в числе n молей и имеющую концентрацию C:

                                                        (9.23)

Энергию Гиббса этой же соли в растворе можно записать через химические потенциалы отдельных ионов: