Равновесная химическая термодинамика. Основы классической термодинамики. Термодинамическое описание химических процессов, страница 4

2.4. Энергия связи

Рассмотрим реакцию диссоциации молекулы AB (при некоторой температуре T):

                                                                              

При этом внутренняя энергия меняется на D_T. Энергия связи A-B равна изменению внутренней энергии при диссоциации AB при T= 0:                     

            (V= const, T= 0, идеальный газ)                                                              (2.14)

Обычно в эксперименте измеряется изменения энтальпии при некоторой температуре, например комнатной (25^o C). Тогда можно вычислить D₂₉₈  и D₀ :

                                                                                   (2.15)

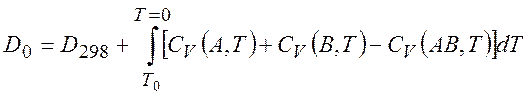                                              (2.16)

2.5. Закон Гесса

Если T= const, то тепловой эффект химической реакции при V= const или P= const не зависит от пути реакции (закон Гесса):

       (T = const)

       (T = const)

В ходе химической реакции

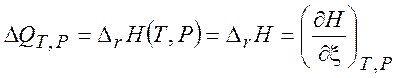
Обозначение для стандартных величин:

Располагая информацией о значениях стандартных энтальпий образования (сгорания, растворения и т.д.) отдельных веществ, можно рассчитывать изменение энтальпии  в самых разнообразных реакциях.

Глава 3. Теория химического равновесия

3.1. Полезная работа химической реакции

Если термодинамическая система снабжена специальным устройством, позволяющим получать полезную работу  (обратимую работу, которую можно было бы использовать в дальнейшем для проведения процесса в обратном направлении), то полная работа равна:

                                                                                                          (3.1)

В качестве полезной работы в химических системах чаще всего выступает электрическая работа. С учетом (3.1) первое начало термодинамики представим в виде

                                                                                                  (3.2)

Для описания необратимых процессов представим второе начало термодинамики в виде

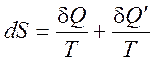                                                                                                              (3.3)

где величина  - некая фиктивная теплота (“некомпенсированная” теплота). Тогда из уравнений (3.2) и (3.3) следует

                                                                                       (3.4)

Из уравнения (3.4) найдем дифференциалы для всех термодинамических потенциалов:

                                                                                           (3.5а)

                                                                                            (3.5б)

                                                                                         (3.5в)

                                                                                          (3.5г)

Уравнения (3.5) позволяют описать термодинамику всех необратимых процессов в закрытых системах.

3.2. Направление самопроизвольного химического процесса. Условия равновесия

Рассмотрим термодинамические системы, в которых не производится полезная работа (= 0). Тогда из уравнений (3.5) имеем:

 ,      ,

 ,                     (направление процесса).

В состоянии равновесия:

      ,      ,     ,      .                         (3.6)

Наиболее часто, чтобы определить направление процесса в закрытых системах, используют энергию Гиббса (при T = const, P = const) .

Рассмотрим систему с одной химической реакцией. Изменения количеств веществ будем описывать с помощью одной химической переменной . Начальные количества реагентов (n_i0) будут при этом параметрами. Тогда

 ,     ,   ,   ,

 ,     ,

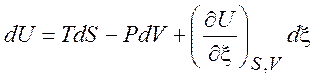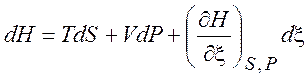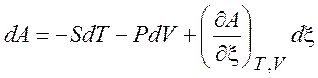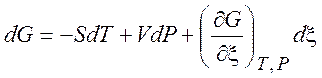 ,     .                      (3.7)

Из уравнений (3.7) следует, что если процесс проводится при постоянных значениях стандартных переменных, то

 ,   ,

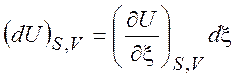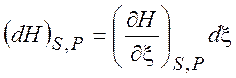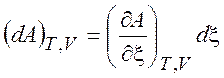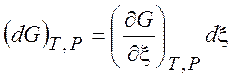,      .                                                    (3.8)

Таким образом,