Равновесная химическая термодинамика. Основы классической термодинамики. Термодинамическое описание химических процессов, страница 8

                                                                                                            (7.17)

Глава 8. Термодинамика растворов неэлектролитов

8.1. Классификация растворов

Общепринятая классификация на основе избыточных функций смешения:

1) идеальные растворы:       ;         ;          ;

2) регулярные растворы:      ;         ;          ;

3) атермальные растворы:   ;         ;          ;

4) реальные растворы:         ;         ;          .

Регулярныерастворы состоят из веществ, молекулы которых имеют близкие размеры; атермальные, наоборот, содержат молекулы с резко различающимися размерами (например, растворы полимерных молекул).

8.2. Давление пара над раствором. Закон Рауля

Рассмотрим раствор двух веществ, находящихся в равновесии с газовой фазой:

В общем случае для неидеального раствора:

                                                                                 (8.1)

и

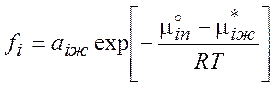                                                                                          (8.2)

Для чистого вещества

 ,   

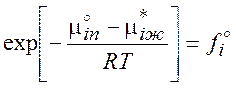                                                                                                 (8.3)

Следовательно, значение летучести над раствором определяет соотношение

                                                                                                                              (8.4)

Вводя коэффициенты летучести и активности, получим

                                                                                                      (8.5)

Если газовая фаза идеальна, то

                                                                                                                (8.6)

Если обе фазы идеальны, то

                       (закон Рауля)                                                                       (8.7)

8.3. Растворимость газа в жидкости. Закон Генри

В равновесии для растворяющегося компонента выполняется равенство

Химический потенциал растворяемого газового компонента в рассматриваемых фазах:

 ,       

Уравнивая химические потенциалы, получаем

                                                                                        (8.8)

Отсюда

             (закон Генри)                                                                                   (8.9)

где К_Г – константа Генри:

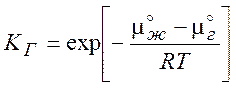                                                                                               (8.10)

В идеальной системе концентрация растворенного газа в конденсированной фазе пропорциональна парциальному давлению газа над раствором:

                                                                                                                    (8.11)

8.4. Регулярные растворы

Термодинамическое описание поведения регулярных растворов обычно основывается на квазикристаллической модели жидкости, в которой предполагается, что каждая молекула находится в одном из узлов квазикристаллической решетки. В случае двухкомпонентного раствора в каждом узле этой решетки можно с вероятностью X₁ обнаружить молекулы первого типа, с вероятностью X₂ – молекулы второго типа. Каждая молекула окружена несколькими (Z) соседями. Будем предполагать, что взаимодействие молекул в растворе ограничивается только взаимодействием с ближайшими соседями. Полная энергия взаимодействия молекул в одном моле раствора:

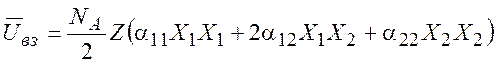                                                   (8.12)

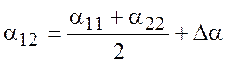                                                                                                (8.13)

Тогда

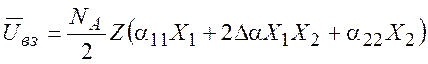                                                               (8.14)

Энергия взаимодействия в исходных чистых веществах до смешения равна

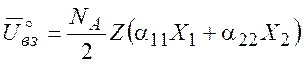                                                                                   (8.15)

Следовательно, внутренняя энергия смешения равна

                                                             (8.16)