Теория работы конусной дробилки с пологим конусом для среднего и мелкого дробления. Определение основных конструктивных параметров сушильного барабана

§17. Теория работы

Рассмотрим теорию работы конусной дробилки с пологим кону­сом для среднего и мелкого дробления, как наиболее пригодную для нужд дорожного строительства.

Определение числа оборотов эксцентриковой втулки. Воспользуемся для этой цели выводами, предложенными проф. Л. Б. Левенсоном. В дробилке с пологим ко­нусом дробимая порода скользит по наклонной плоскости дробя­щего конуса, подвергаясь действию сил тяжести и сил инерции.

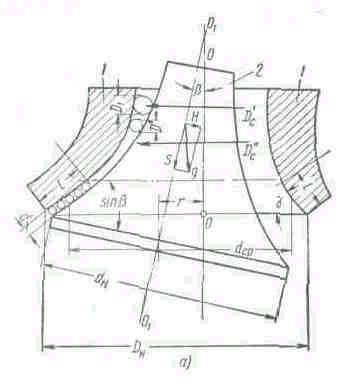
Фиг. 41. Процесс дробления в дробилке с пологим конусом:

1- неподвижный конус;    2- дробящий конус.

Силы инерции возникают вследствие принудительных круговых качаний геометрической оси дробящего конуса 2 (фиг. 41) и под действием возможного добавочного вращения дробящего конуса вокруг своей оси, а также возникающей при этом сложном движении кориолисовой силы инерции.

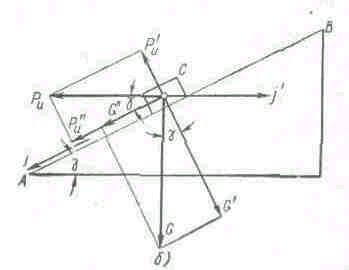
Процесс дробления и разгрузки продукта в конусной дробилке с пологим конусом показан на фиг. 41, а, где l – длина зоны парал­лельности. Назначение этой зоны – обеспечить получение кусков продукта не более минимальной ширины этой зоны d. Для выпол­нения этого условия время прохождения куска породы в зоне дли­ной l должно быть не меньше времени одного полного качания дро­бящего конуса, т. е. не меньше времени полного оборота эксцентрика. Ввиду того, что центробежная сила инерции Р_и теоретически не ока­зывает влияния на скольжение куска породы по дробящему конусу 2, а кориолисова сила инерции незначительна, можно ими пренебречь и рассматривать движение куска породы как простое скольжение вниз по наклонной плоскости АВ (фиг. 41, б) при угле наклона g с ускорением

,

где m - коэффициент трения между куском породы С и поверх­ностью А В дробящего конуса.

Время t прохождения куском С пути длиной l при равномерно ускоренном движении определим из выражения

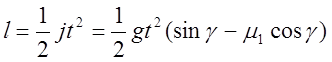   (27)

Принимают l»0,08 d_н , где d_н – нижний диаметр дробящего конуса в см.

Исходя из приведенного выше условия правильной работы дробилки время t должно быть не меньше t₂ – времени одного полного качания дробящего конуса 2. Так как t₂=, получим из формулы (27)

l³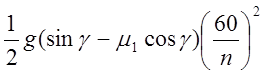

Из последней формулы получаем

,

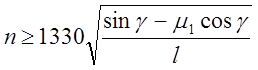где l – длина зоны параллельности в см;

g= 981 см/сек²;

g - угол наклона образующей дробящего конуса 2 в зоне параллельности, g= 41°;

m₁ – коэффициент трения, m₁» 0,36.

В приведенном выводе мы пренебрегли влиянием сил инерции. Однако существует ограничительное условие для наибольшей вели­чины центробежной силы инерции Р_u, а именно: для возможности действительного скольжения куска породы С вниз по пологому конусу 2 без отрыва от него должно быть соблюдено условие

,

где Р_u^¢ - нормальная составляющая горизонтальной силы инер­ции,

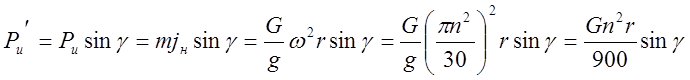
где Gи  т — вес и масса куска камня;

j_н — центростремительное ускорение;

w — угловая скорость в радианах в секунду;

п — число оборотов конуса в минуту;

r — эксцентриситет в м.

Так как нормальная составляющая веса G равна

,

получим

,

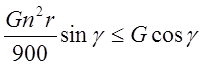откуда

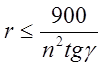
Определение производительности дробилки. Воспользовавшись фиг. 41, а, определим объем породы, который провалится за время одного полуоборота в зоне отхода конуса (головки) от корпуса. Это будет объем полукольца, равный

V=.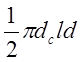

Здесь

,

где d_н – номинальный размер дробилки, равный диаметру нижнего основания дробящего конуса 2;

l – длина зоны.

Зная величину V, определяем часовую производительность дробилки с пологим конусом в м^з/час:

 м³/час.                                           (28)

При длине зоны параллельности l = 0,08d_н формула (28) примет следующий вид:

 м³/час.

где m — коэффициент разрыхления породы в движении;

m= 0,25¸0,45;

d и d_н– в м.

Определение мощности двигателя. Для определения мощности двигателя для дробилок с пологим конусом можно воспользоваться формулой инж. А. А. Липмана, но обязательно с проверкой полу­ченных результатов путем сравнения их с имеющимися практиче­скими данными. Формула А. А. Липмана основывается на объемной теории дробления и на методике, аналогичной той, которую при­менил проф. Л. Б. Левенсон для дробилок с крутым конусом.

А. А. Липман предлагает положить в основу расчета не один ряд захваченных дробилкой кусков исходного материала, а два или три ряда.

Принимаем, что захватываются два ряда (фиг. 41). Фактический объем раздробленного материала за один оборот дробящего конуса

,

где

,

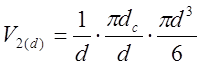а так как d_ср» d_н , а l»0,08d_н, то получим

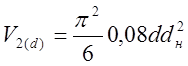
Величина V_1(D) определяется по формуле

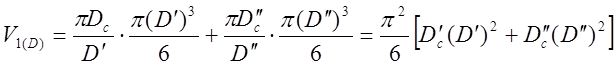
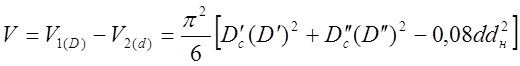
Поскольку разность второго и третьего членов, заключенных в квадратные скобки, мала по сравнению с первым членом, от­брасываем ее.

Тогда

.

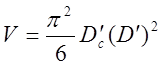Работа дробления за один оборот дробящего конуса

,

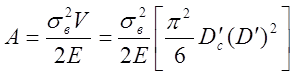а расход мощности на дробление

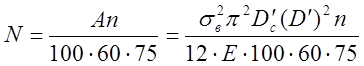  л. с.

С учетом к. п. д. привода

,

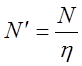где h - к. п. д. привода, h =0,8 ¸0,9.

Формула Л. Б. Левенсона, выведенная теоретическим путем для дробилок с крутым конусом, не пригодна для расчета дробилок с пологим конусом, хотя при приближенном рассмотрении механики происходящего процесса часто дает результаты, близкие к действи­тельности.

Определение усилий в элементах конусной дробилки с пологим конусом. Определить усилия в элементах можно по усилию сжатия предохранительных пружин 24 (см. фиг. 37), установленному экспе­риментальным путем.