Схема общей нагруженности дробилки в процессе дробления представлена на фиг. 42.
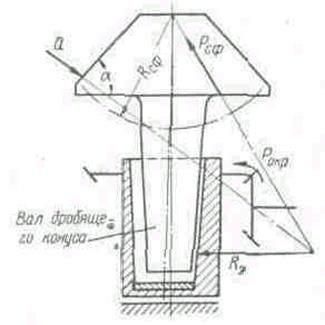
Фиг. 42. Схема общей нагруженности конусной дробилки с пологим конусом в процессе дробления.
В дробилках с пологим конусом, изготовляемых нашей промышленностью, усилия, возникающие при работе дробилки, стремятся приподнять верхнюю часть машины, чему препятствуют пружины. При нормальной работе дробилки пружины удерживают верхнюю часть в постоянном контакте со станиной. При попадании же недробимого куска усилия от первоначальной затяжки пружин оказываются недостаточными для удержания верхней части, которая несколько приподнимается, вызывая дополнительное сжатие пружин. Зная усилие от первоначальной затяжки каждой пружины и количество их, можно определить наибольшее рабочее усилие дробления (фиг. 43) по формуле
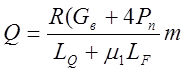, (29)
где R – плечо пружины (берется из чертежа);
Cв – вес верхней части дробилки в т;
Pn – усилие в каждой группе пружин;
LQ – плечо усилия дробления относительно точки А поворота верхней части;
m1 – коэффициент трения камня о металл; m1 = 0,2;
LF– плечо силы трения F=m1Q.
Значения величин, входящих в формулу (29), могут быть найдены следующим образом:
,
где Р – первоначальная сила натяжения одной пружины, равная для дробилки СМ-560 5,12 т и для дробилки СМ-561 2,1 т;
п — число пружин в группе.
,
где ln – плечо каждой группы пружин.
На основании схемы размещения пружин, приведенной на фиг. 43, б, можно найти значения lдля каждой группы пружин:
;
;
;
Для случая попадания в камеру дробления недробимого материала дробящее усилие Q¢ определяется по формуле
,
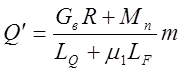где Mn – момент, создаваемый пружинами, равный
.
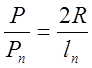и 
,
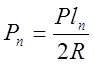здесь Pn – усилие в группе пружин при полном их сжатии.
|
|
|
|
Фиг. 43. Схемы к определению усилия дробления дробилки с пологим конусом:
а - схема к определению Qдр и Q¢др; б – схема размещения пружин.
При попадании недробимого тела усилия в каждой группе пружин различны и зависят от удаленности пружин от места попадания недробимого материала. При этом зависимость принимается прямой. График распределения усилий в пружинах при попадании недробимого материала приведен на фиг. 43, б.
§ 19. Теория работы.
Рассмотрим условия, определяющие возможность работы валковой дробилки, ее теоретическую производительность и необходимую мощность двигателя (по Л. Б. Левенсону).
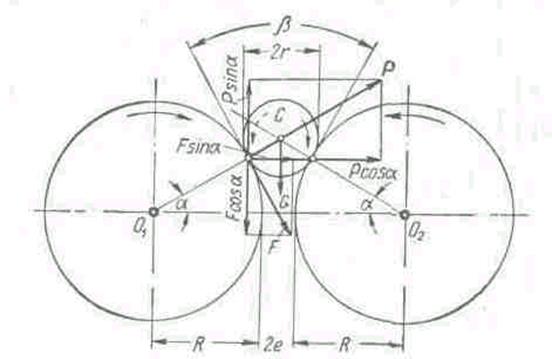
Фиг. 46. Схема работы валковой дробилки.
Для возможности втягивания куска камня С в пространство между валками (фиг. 46), что определяет возможность процесса дробления, должно быть соблюдено условие
,
откуда
,
а так как
,
где j - угол трения,
то
или
, (30)
т. е. угол захвата не должен быть больше угла трения, аналогично полученному по формуле (10) для щековых дробилок.
Часто углом захвата для валковых дробилок называют угол b=2a. В этом случае формула (30) примет вид
.
Для гранита и известняка m1 = 0,30¸0,35 и среднее значение угла a должно быть 18°.
Раздавливающее действие валков на кусок породы С в момент его захвата определяется горизонтальными составляющими Pcosa и m1Psina=Fsina от обоих валков.
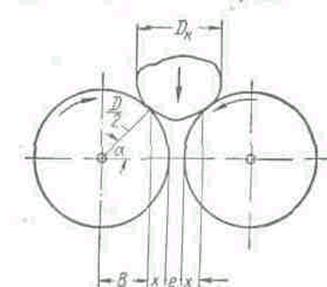
Фиг. 47. Схема к определению размера камня для валковой дробилки.
Для эффективной работы валковой дробилки при соблюдении условия, что a £ j, и расстоянии 2е между валками необходимо, чтобы диаметр камня Dк, поступающего в дробилку, удовлетворял следующему условию:
,
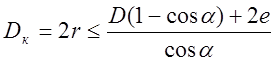(31)
где D = 2R – диаметр валков.
Если принять для гранита и известняка угол захвата a = 18° и cos a » 0,95, то формула (31) преобразуется:
.
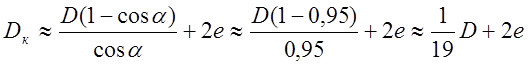При сдвинутых валках (2е = 0)
.
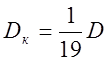Размер конечного продукта теоретически равен нулю, в действительности же он зависит от степени жесткости буферных пружин, надавливающих на подвижный валок.
По данным американской фирмы «Айова» максимальный размер захватываемых камней для дробилки с одним гладким, а другим рифленым валком Dk = 1,5 (2х ± с) (фиг. 47). В расчетах принимаем с = 2е. Тогда получаем
Dk = 1,5(2х ± 2е).
Согласно схеме на фиг. 47 получаем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
