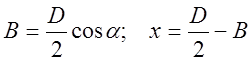
Определив значение х и приняв с = 2е, находим
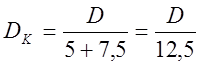
Производительность валковой дробилки определяем как непрерывную ленту поперечного сечения F = 2Le (см. фиг. 44, г), выходящую из выходной щели длиной L и шириной 2е со скоростью v м/сек, равной окружной скорости валков
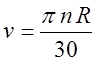
Тогда получим
, (32)
где m - коэффициент разрыхления движущегося продукта, для пород средней твердости m = 0,2 ¸ 0,3, для вязких пород m = 0,5 ¸ 0,6. Вообще величину mможно брать тем больше, чем меньше величина 2е и размер кусков 2r и чем мягче пружины. Величина mзаметно уменьшается с увеличением степени измельчения и твердости дробимого материала.
Для получения более точной формулы производительности следует учесть неизбежное при дроблении раздвигание валков на величину р. При наличии пружины р = 0,25 – 16 мм. По практическим данным
.
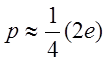Вводя эту поправку в формулу (32) и принимая 2е=d,
где d – поперечник готового продукта, получим
,
при
,
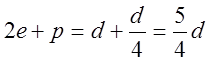
где все линейные размеры в м.
Из приведенной формулы видно, что производительность прямо пропорциональна числу оборотов валка в минуту.
Предельное число оборотов валка не должно превышать величины, определяемой формулой
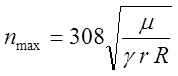
где g - удельный вес камня в кг/м3.
Мощность двигателя. Мощность в валковой дробилке с гладкими валками расходуется на:
- работу дробления N1;
- работу трения породы на валках N2;
- работу на трение шеек (цапф) валков в подшипниках N3.
Используя формулу (6) и подсчитав объем раздробляемой породы V по методике для щековых дробилок [см. формулу (19)], получаем
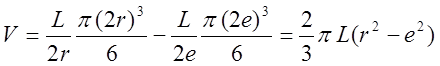
Работа дробления для одного ряда кусков диаметром Dk= 2r, захваченных валками, будет
,
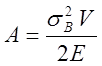а при непрерывном и равномерном питании работа дробления при одном обороте валков
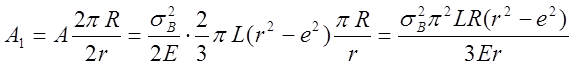
Потребная мощность двигателя на дробление
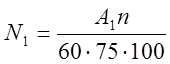л. с.
После подстановки значения А1 и некоторых преобразований получаем
,
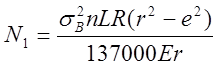где величины L, R, r, e – в см; sи Е — в кг/см2. Эту формулу можно упростить, приняв приближенно, что
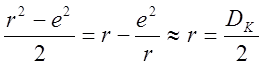
тогда
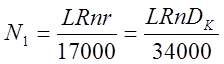
где DK = 2r, а величины L, R и r – в см.
Между породой и валком происходит трение на том же пути (на угле a поворота валков), на котором силой Р производится работа раздавливания А1. Предположим, что отношение работы трения к работе раздавливания
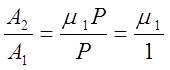
тогда мощность, требуемая на преодоление трения,
(34)
где m- коэффициент трения породы о валок, m1 » 0,3.
Расход энергии на трение шеек валков в подшипниках может быть принят с некоторыми допущениями (по Л. Б. Левенсону),
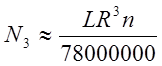, (35)
где величины L и R – в см.
Формула (35) выведена для подшипников скольжения. При подшипниках качения N'3 = 0,1N3. Общая потребная мощность двигателя
N = N1 + N2 + N3.
Формулы (33) и (34) носят приближенный характер и дают достаточно точные данные только для дробилок средних размеров и при дроблении пород с пределом прочности
sв = 1250 кг/см2 и E = 200000 кг!см2.
Для определения производительности и мощности двигателя валковых дробилок существует также ряд эмпирических формул, который приводится в специальной литературе.
Теория молотковой дробилки разработана еще недостаточно, и не существует точных расчетных формул, позволяющих определить ее основные параметры – наивыгоднейшую скорость, теоретическую производительность, мощность двигателя, действующие усилия. Но некоторые вопросы динамики, которые имеют особую важность вследствие быстроходности дробилки, разработаны проф. М. М. Гернетом.
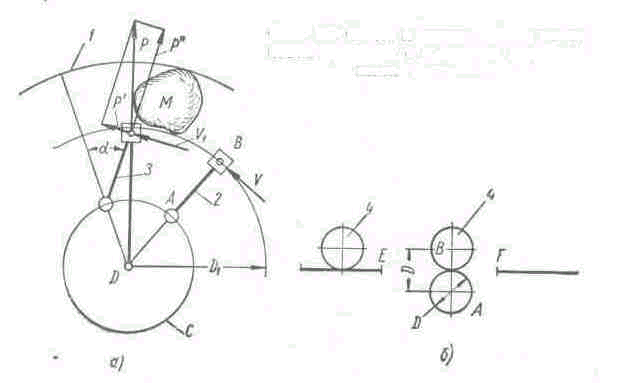
Фиг. 52. Схема к теории работы молотковой дробилки с шарнирно укрепленными молотками.
В процессе измельчения в молотковой дробилке с шарнирно укрепленными молотками различают следующие четыре стадии:
1. Материал разбивается ударами быстро вращающихся молотков, наносимыми непосредственно по кускам при их поступлении в дробилку (удары на лету);
2. Материал разбивается от удара о броневые плиты, на которые он отбрасывается молотками;
3. Материал, поддерживаемый броневыми плитами, как наковальней, разбивается ударами молотков;
4. Материал крошится между молотками и колосниками внизу машины.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.