Четвертая стадия измельчения – последняя, так что размер продукта дробления определяется величиной зазора между внутренней цилиндрической поверхностью колосников и концами молотков.
Наиболее эффективным считается дробление ударами на лету. При питании крупными кусками большое значение имеет дробление на плитах как на наковальне, а при мелком – крошение (раздавли-вание с истиранием) на колосниковой решетке.
Определение углов отклонения молотка при ударе. Молотки В (фиг. 52) дробилки, вращающиеся вокруг шарниров А, под влиянием центробежной силы, возникающей при вращении ротора, расходятся и занимают положение по направлению радиусов. Молотки ударяют поступающие в дробилку куски камня, отчасти разбивают их и отбрасывают к броне 1, которая устанавливается так, чтобы зазор между броней и окружностью, описываемой молотками В, постепенно уменьшался в такой степени, чтобы куски С хорошо заклинивались между броней и молотками (на фиг. 52 уменьшение зазора не показано). Постепенное уменьшение зазора также важно в том отношении, чтобы дробилка могла раздроблять куски разного диаметра.
После удара по куску материала молоток теряет часть своей кинетической энергии и начинает отклоняться от радиального направления.
Центробежная сила Р препятствует такому отклонению, и молоток, отклонившись до своего крайнего положения на угол а, будет возвращаться обратно, совершая колебания. Необходимо, чтобы угол а не превосходил известных норм для данной дробилки и чтобы молоток достаточно скоро возвращался в свое нормальное радиальное положение.
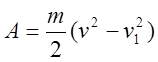, (36)
где т – масса молотка, сосредоточенная в точке В (приведенная масса);
v – скорость молотка до удара;
v1 – скорость молотка после удара.
Соответствующая работа в относительном движении молотка выразится так:
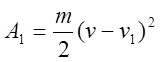, (37)
Центробежную силу Р (фиг. 52), действующую на молоток 3 в отклоненном положении, разложим на силы Р' и Р".
Работу перемещений силы Р' в относительном движении можно выразить так:
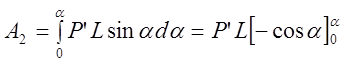
При a= 0, соs a = 1 и А2 = 0, следовательно,
,
где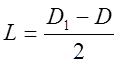 
-
плечо молотков. Принимая, что А1 = А2. для угла
отклонения a, получаем
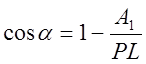
Величина центробежной силы Р определяется по известному уравнению механики
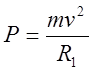
где R1 –
радиус окружности, описываемой молотками,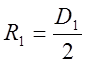 
.
Приведенные формулы дают результат тем более точный, чем больше отношение вращающейся массы дробилки к массе молотка и чем меньше угол отклонения a.
Производительность. При ударе молотка по куску материала работа удара расходуется на работу деформации разбиваемого куска, работу деформации молотка и работу деформации основания, в данном случае – броневой плиты дробилки и самой дробилки в целом.
Удельная работа деформации при разрушении, т. е. работа, приходящаяся на 1 см3 раздробленного материала, выражается так:
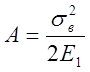
где sв - предел прочности камня в кг/см2;
Е1 – модуль упругости камня в кг/см2.
При этом предполагается, что материал подчиняется закону Гука. Исследования указывают также на некоторое увеличение предела прочности при ударе, которым пренебрегаем ввиду малого значения.
Согласно теории Риттингера (см. § 9) при каждом дроблении материала на куски с размерами, вдвое меньшими первоначальных, поглощается работа 3А, где А – работа, требуемая для разделения по одной плоскости.
Если, например, после дробления куски будут иметь размер в 2 раза меньше первоначальных, то число кусков будет
т = 23а,
а работа, поглощаемая при таком раздроблении,
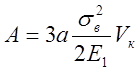(38)
Определив работу деформации, необходимую для дробления куска, можно далее определить наибольшие размеры куска, который может быть раздроблен дробилкой данной конструкции.
Задаваясь наибольшими допустимыми углами a отклонения молотков при ударе о разбиваемый кусок, можно определить по уравнению (37) работу молотка в относительном движении.
Затем определяется скорость v1 молотка после удара по формуле (36) и далее работа деформации при ударе, равная потерянной живой силе, по формуле (38).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.