Застосування теорії чисел в криптографії

1 Подільність цілих чисел.

1.1 Основні поняття та теореми.

Теорія чисел розглядає властивості цілих чисел, тобто чисел класу . Сума та добуток цілих чисел є цілі числа, але про результат ділення двох цілих чисел такого стверджувати вже не можна.

Означення. Для довільних цілих чисел  і  визначається, що  ділить  ( ділиться на ), якщо існує таке ціле число , для якого виконується рівність:

Позначається цей факт так: . При цьому  називається дільником , число  за таких умов називається кратним .

Власним дільником  називається будь який додатній дільник , що не є рівним . Нетривіальним дільником  називається будь який додатній дільник , який не дорівнює 1 та .

Прости числом за означенням є ціле число, яке має за дільники тільки 1 та . Ціле число, яке має хоча б один нетривіальний дільник, називається складеним числом.

Властивості подільності цілих чисел.

1.  Якщо  і  - будь яке додатне ціле число, то.

2.  Якщо  та , то .

3.  Якщо  та , то .

4.  Узагальнення: якщо у рівності  про всі числа, крім одного відомо, що вони кратні числу , то і це останнє є кратним .

Теорема про ділення з залишком. Будь яке ціле число  єдиним способом подається за допомогою додатного цілого числа  рівністю:

,

де  - неповна частка,  - залишок

Очевидно, що за умови   є повна частка, а .

Якщо просте число  є неоднократним дільником довільного цілого числа  (число  ділиться на  -разів,  - ціле невід’ємне число), то цей факт будемо позначати так: . В цьому випадку , а .

1.2 Найбільший спільний дільник (НСД).

Не звужуючи загальної теорії будемо у подальшому розглядати тільки додатні дільники чисел.

1. Будь яке ціле , яке одночасно ділить числа  носить назву спільного дільника цих чисел. Найбільший із всіх дільників носить назву найбільший спільний дільник (НСД) та позначається

2. Якщо , то числа  - взаємо прості, якщо кожне число з наведеного набору є взаємо простим з кожним іншим числом цього набору, то ці числа – попарно прості. Попарно прості числа є одночасно і взаємо простими, але не навпаки.

Приклад: Числа 6, 10, 15 – взаємо прості, бо , але вони не попарно прості. Числа 7, 13, 23 – попарно прості, бо , і одночасно вони взаємо прості.

НСД двох цілих чисел а і b.

1. Якщо , то  і кількість дільників у чисел  та  співпадає з кількістю дільників .

2. Якщо , то кількість дільників  співпадає із кількістю спільних дільників  та , зокрема

 ( витікає з властивості 4. п.1.1)

3. Якщо

Алгоритм Евкліда для знаходження НСД двох чисел  і .

Цей алгоритм ґрунтується на попередніх твердженнях. Розглянемо  та , причому . Тоді можна записати обмежений ланцюжок ділень з залишком:

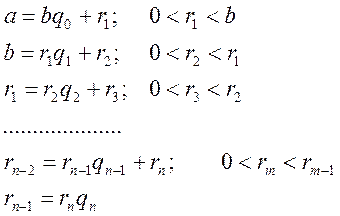
Останнє ділення – ділення без залишку, тобто

Досліджуючи цей ланцюжок з останнього ділення уверх, отримаємо:

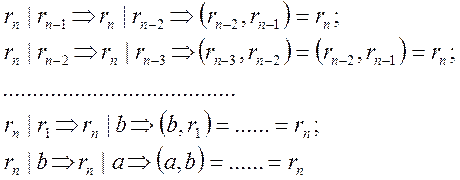
Отже,

-  сукупність дільників  та  співпадає з сукупністю дільників їх НСД.

-  НСД  та  дорівнює останньому ненульовому залишку в ланцюжку ділень за алгоритмом Евкліда.

Узагальненням алгоритму Евкліду буде теорема:

Спільний дільник двох довільних цілих чисел  можна єдиним способом подати лінійною комбінацією цих чисел:

,  одночасно.

Доведення теореми витікає з алгоритму Евкліду, якщо всі залишки, починаючи з  поступово виразити через попередні залишки, а потім і через  та .

Приклад: 1. Знайти НСД a=648 та b=261. 2. Знайти .

Розв’язання:

1. Шукаємо НСД

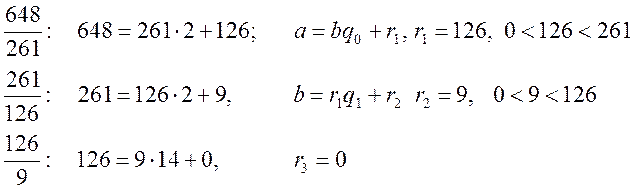
Останній ненульовий залишок - . Отже,

2. Шукаємо подання НСД лінійною комбінацією:

Отже

Деякі властивості НСД:

1.  Якщо .

2.  Якщо 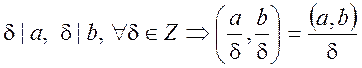, зокрема 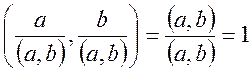, тобто два будь яких цілих числа, поділених на НСД цих чисел є взаємо простими числами.

3.  Якщо ;

4.  Якщо ;

5.  Якщо  взаємо прості з кожним з , то добуток  взаємо простий з добутком