4.
Якщо один з боків конгруенції і модуль діляться на
деяке число, то і інший бік ділиться на це число. ![]() (за 3-ю властивістю
подільності)
(за 3-ю властивістю
подільності)
5.
Якщо ![]()
1. Повна система лишків.
Усі числа, які
мають однаковий залишок ![]() від ділення на деякий
модуль
від ділення на деякий
модуль ![]() створюють клас чисел по модулю
створюють клас чисел по модулю ![]() . Усі числа цього класу можна отримати з
формули ділення числа із залишком
. Усі числа цього класу можна отримати з
формули ділення числа із залишком ![]() , якщо надавати
неповній частці
, якщо надавати
неповній частці ![]() усіх значень з множини цілих
чисел.
усіх значень з множини цілих
чисел.
![]() різним залишкам від ділення за модулем
різним залишкам від ділення за модулем ![]()
![]() будуть відповідати
будуть відповідати ![]()
![]() різних класів. Модуль
різних класів. Модуль ![]() за залишки може мати числа
за залишки може мати числа ![]() . Отже, кількість таких класів за
довільним цілим модулем
. Отже, кількість таких класів за
довільним цілим модулем ![]() становить
становить ![]() .
.
Кожне число з
певного класу носить назву лишку відносно усіх інших чисел класу. Якщо ![]() то лишок
то лишок ![]() є найменшим
додатним лишком.
є найменшим
додатним лишком.
Найменший лишок за
абсолютною величиною називається абсолютно найменшим лишком і
позначається ![]() .
.
Приклад: Візьмемо за модуль число ![]() . Тоді найменшими
додатними лишками будуть числа
. Тоді найменшими
додатними лишками будуть числа ![]() . Для кожного з них
можна записати клас чисел по модулю 7:
. Для кожного з них
можна записати клас чисел по модулю 7:
|
|
|
При цьому,
створюючи відповідний клас ![]() , неповна частка
, неповна частка ![]() пробігає всю множину цілих чисел.
пробігає всю множину цілих чисел.
Абсолютно
найменшими лишками за модулем 7 будуть числа ![]()
Якщо порівняти їх з
найменшими додатними лишками, можна помітити, що для лишків 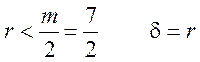 , а для
, а для 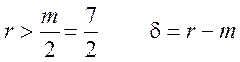 .
.
В такий спосіб будується
множина абсолютно найменших лишків за будь яким модулем. Якщо модуль ![]() є парним числом, то для
є парним числом, то для 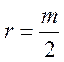 можна за абсолютно найменший лишок брати
або
можна за абсолютно найменший лишок брати
або ![]() , або
, або ![]() .
.
Якщо з кожного
класу лишків узяти по одному числу, то будемо мати повну систему лишків.
Кількість повної системи лишків за модулем ![]() є
є ![]() . Звернемо увагу на те, що числа з двох
різних класів не конгруентні, бо мають різні залишки від ділення на модуль.
. Звернемо увагу на те, що числа з двох
різних класів не конгруентні, бо мають різні залишки від ділення на модуль.
Найменші додатні
лишки ![]() складають повну систему. Абсолютно
найменші лишки
складають повну систему. Абсолютно
найменші лишки 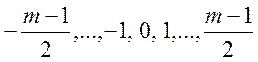 для
для ![]() непарного
і
непарного
і 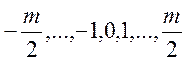 для
для ![]() парного
теж складають повну систему лишків.
парного
теж складають повну систему лишків.
Узагальнення:
1. Будь які ![]() чисел, які попарно не конгруентні за
модулем
чисел, які попарно не конгруентні за
модулем ![]() складають повну систему лишків за цим
модулем.
складають повну систему лишків за цим
модулем.
2. Якщо ![]() і у виразі
і у виразі ![]()
![]() пробігає усі значення повної системи
лишків за модулем
пробігає усі значення повної системи
лишків за модулем ![]() , то
, то ![]() теж
приймає усі значення повної системи лишків.
теж
приймає усі значення повної системи лишків.
Приклад. Перевірити, чи складає сукупність чисел ![]() повну
систему лишків за модулем 8.
повну
систему лишків за модулем 8.
Розв’язання: Повна
система лишків за модулем 8, складена з найменших додатних лишків є ![]() . Необхідно впевнитися, що дана сукупність
чисел складає конгруенції за модулем 8 такі, які входять до повної системи.
. Необхідно впевнитися, що дана сукупність
чисел складає конгруенції за модулем 8 такі, які входять до повної системи.
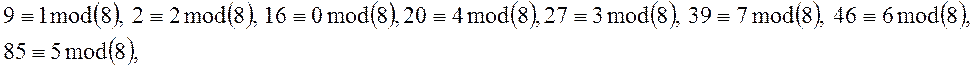 .
.
Дана сукупність чисел конгруентна лишкам з повної системи, але розташованим у іншому порядку. Отже вихідна система є повною системою лишків.
2. Зведена система лишків.
Згідно із
властивістю лишків числа одного і того ж класу лишків за модулем ![]() мають з
мають з ![]() однаковий
НСД:
однаковий
НСД: ![]() . Серед множини класів лишків за певним
модулем
. Серед множини класів лишків за певним
модулем ![]() розглянемо такі класи лишків, у яких
розглянемо такі класи лишків, у яких ![]() , тобто класи , взаємо прості з модулем
, тобто класи , взаємо прості з модулем ![]() . Якщо взяти з кожного такого класу по
числу, то складеться зведена система лишків за модулем
. Якщо взяти з кожного такого класу по
числу, то складеться зведена система лишків за модулем ![]() . Зазвичай зведену систему лишків виділяють
з найменшої додатної системи лишків, або з абсолютно найменшої системи лишків.
. Зазвичай зведену систему лишків виділяють
з найменшої додатної системи лишків, або з абсолютно найменшої системи лишків.
Оскільки кількість
чисел від 0 до ![]() взаємно простих з
взаємно простих з ![]() визначається функцією Ейлера
визначається функцією Ейлера ![]() , то відповідно, і кількість чисел у
зведеній системі, і кількість класів, що відповідають зведеній системі
визначаються функцією Ейлера
, то відповідно, і кількість чисел у
зведеній системі, і кількість класів, що відповідають зведеній системі
визначаються функцією Ейлера 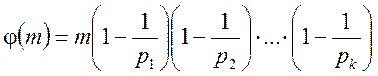 , де
, де ![]() - прості числа з канонічного розкладання
- прості числа з канонічного розкладання ![]() .
.
Приклад: 1. ![]() , отже зведена система лишків за модулем
130 складається з 48 чисел, взаємно простих з 130.
, отже зведена система лишків за модулем
130 складається з 48 чисел, взаємно простих з 130.
2. ![]() , отже зведена система лишків за модулем 16
складається з 8 чисел, взаємно простих з 16, ці числа такі:
, отже зведена система лишків за модулем 16
складається з 8 чисел, взаємно простих з 16, ці числа такі: ![]() . Ці числа і складають зведену систему
лишків для числа 16.
. Ці числа і складають зведену систему
лишків для числа 16.
Узагальнення:
1. Будь які ![]() чисел, попарно не порівняльні за модулем
чисел, попарно не порівняльні за модулем ![]() та взаємно прості з модулем, створюють
зведену систему лишків.
та взаємно прості з модулем, створюють
зведену систему лишків.
2. Якщо ![]() і
і ![]() пробігає
усі значення зведеної системи лишків за модулем
пробігає
усі значення зведеної системи лишків за модулем ![]() , то
, то ![]() теж приймає усі значення повної системи
лишків.
теж приймає усі значення повної системи
лишків.
Розглянемо повну систему лишків (наприклад
повну систему найменших додатних лишків) за модулем ![]() , яка
створює
, яка
створює ![]() попарно не конгруентних класів. Позначимо
цю систему:
попарно не конгруентних класів. Позначимо
цю систему:
![]() .
.
На такій системі, враховуючи усі вище наведені властивості, можна розглянути дві бінарні операції: додавання та множення.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.