Застосування теорії чисел в криптографії, страница 12

Маємо . Отже спочатку шукаємо розв’язок конгруенції

.

По-перше, спростимо її: , або . Маємо розв’язок:

. Підставимо цей  у конгруенцію .

 - не ділиться на

. Поділимо конгруенцію на :

.

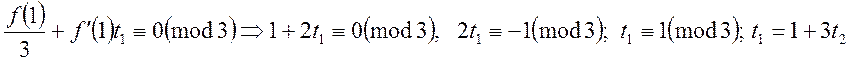Підставимо значення  у формулу для : . Отже знайшли розв’язок .

 підставимо до конгруенції .

. Поділимо конгруенцію на :

.

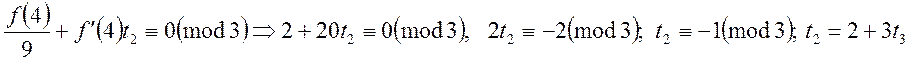Отже розв’язком конгруенції  буде клас чисел . Розв’язок єдиний.

5.4 Конгруенції 2-го степеня .

Загальний вигляд конгруенції:

                                                                                           (1)

Теорема 1. Конгруенцію (1) завжди можна звести до конгруенції виду

                                                                                                     (2)

Дійсно, за властивостями конгруенцій, які відповідають зміні модуля конгруенції, можемо помножити усі складові конгруенції на множник :

Виділимо ліворуч повний квадрат:

Позначимо , отримали вираз (2).

Якщо конгруенція (2) має розв’язок , то можна знайти розв’язок  за умови, що . Тобто за виконання додаткової умови розв’язок (2) є розв’язком (1). Якщо (2) не має розв’язку, то (1) теж немає розв’язку.

Наслідок: Якщо модуль є складеним числом , то розв’язання конгруенції (2) зводиться до розв’язання системи конгруенцій виду:

,

де  - просте число.

Розглянемо розв’язання (2) у випадках:

1.  Модуль  - просте непарне число в першій степені.

2.  Модуль  - просте непарне число в степені .

3.  Модуль

5.5 Квадратична конгруенція за простим непарним модулем

Розглянемо конгруенцію

                                                                                                           (3)

Якщо , то (3) має один розв’язок.

Теорема 2. Критерій Ейлера. Якщо  в конгруенції (3) не ділиться на , тобто , то відповідна конгруенція має 2 різних розв’язки, якщо

,

або зовсім немає розв’язків, якщо

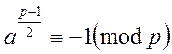
Доведення: Розглядаємо конгруенцію (3) за прости непарним модулем.

Оскільки , то за теоремою Ферма . Оскільки в нашому випадку  завжди парне, то вірним буде подання:

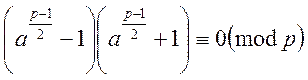
Якщо добуток ділиться на просте число, значить обов’язково хоча б один з множників ділиться на це число. Одночасно числа 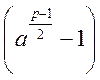 та  на  ділитися не можуть, бо їхня різниця дорівнює 2, не ділиться на . Отже можливі два випадки:

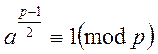, або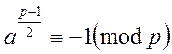

Тепер згадаємо, що коли (3) має розв’язок, то існує  (та ) такий, що , причому, оскільки , то і . Для таких конгруенцій за властивостями можливе піднесення до цілого степеня. Піднесемо конгруенцію до степеня 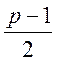, отримаємо:

.

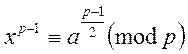За теоремою Ферма з урахуванням  маємо , отже, виходячи з існування розв’язку  конгруенції (3), отримали:

.

Висновок: якщо (3) має розв’язки, то для неї виконується конгруенція . Коренів конгруенція має рівно 2 класи, створені на лишках з повної системи абсолютно найменших  та  (або  та  з повної системи найменших лишків) модуля , оскільки  

Очевидно, що  та  різні, тобто не конгруентні між собою, інакше б виконувалася конгруенція , тобто ділився б на , а це протиріччя до вихідної конгруенції. Більше коренів бути не може за теоремою про кількість коренів конгруенції з простим модулем.

Відповідно, іншій випадок - 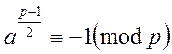 - виконується тільки для таких , для яких конгруенція (3) не має розв’язку.

Тепер прояснимо питання кількості чисел , для яких конгруенція (3) буде мати розв’язки. Очевидно, що  належить до класів, створених на повних системах абсолютно найменших або найменших лишків без нуля. Для простого модуля  таких класів . Але вище було відмічено, що  та  (або  та ) дають однакові квадрати, тобто . Отже, будемо мати чисел, для яких конгруенція (3) має розв’язок, рівно половину з кількості елементів у повній системі лишків без нуля, тобто рівно 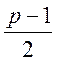 лишки з повної системи лишків відповідають (3), а інша половина – ні. Нагадаємо, що  - непарне, отже 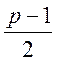 - ціле число.

Приклад. Розглянемо повну систему абсолютно найменших лишків для чисел 5 та 7 і з’ясуємо, для яких лишків конгруенція (3) буде мати розв’язок, а для яких ні. В дужках будемо подавати відповідні лишки з повної системи найменших лишків.

 повна система абсолютно найменших лишків без нуля:  . Відповідні квадрати:    .

Отже, якщо в (3) модуль дорівнює 5, а права частина , то конгруенція розв’язок має. Для  розв’язків немає. Тобто для 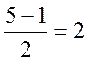 лишків розв’язок є, для 2-х – немає.