![]() повна система абсолютно
найменших лишків без нуля:
повна система абсолютно
найменших лишків без нуля: ![]()
![]() . Відповідні квадрати:
. Відповідні квадрати: ![]() (
(![]()
![]()
![]() )
)
Отже, якщо в (3) модуль дорівнює 7, а права
частина ![]() , то конгруенція розв’язок має. Для
, то конгруенція розв’язок має. Для ![]() розв’язків немає. Тобто для
розв’язків немає. Тобто для 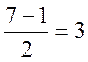 лишків розв’язок є, для 3-х – немає.
лишків розв’язок є, для 3-х – немає.
Висновок. Серед
повної системи лишків для простого непарного модуля ![]()
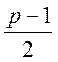 елементів відповідає конгруенції (3) і
елементів відповідає конгруенції (3) і 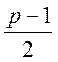 елементів не відповідає.
елементів не відповідає.
Для таких елементів, що відповідають, виконується конгруенція

Для інших – конгруенція
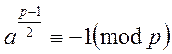
Означення: Значення
![]() , для якого конгруенція (3) має розв’язок,
називається квадратичним лишком модуля
, для якого конгруенція (3) має розв’язок,
називається квадратичним лишком модуля ![]() . Якщо
для деякого
. Якщо
для деякого ![]() конгруенція (3) розв’язку немає, то
конгруенція (3) розв’язку немає, то ![]() носить назву квадратичного
нелишку модуля
носить назву квадратичного
нелишку модуля ![]() .
.
Наслідок з критерію Ейлера: У повній системі лишків простого непарного модуля ![]() кількість лишків завжди дорівнює кількості
нелишків, а саме
кількість лишків завжди дорівнює кількості
нелишків, а саме 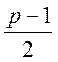 .
.
Теорема 3. (Теорема Ейлера). Добуток двох лишків або двох нелишків за модулем ![]() є лишок. Добуток лишку на нелишок за модулем
є лишок. Добуток лишку на нелишок за модулем ![]() є нелишок.
є нелишок.
Доведення: З критерію Ейлера:
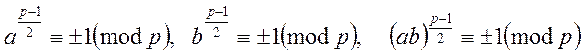 ,
,
„+” буде за умови, що знаки біля 1 однакові, „-” – різні.
Означення: Розглянемо
конгруенцію ![]() (1)
(1)
Якщо ![]() простий
непарний модуль і
простий
непарний модуль і ![]() , символом Лежандра називається
величина
, символом Лежандра називається
величина
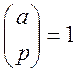 , якщо
, якщо ![]() - квадратичний
лишок за модулем
- квадратичний
лишок за модулем ![]() і
і 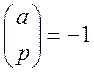 ,
якщо
,
якщо ![]() - квадратичний
нелишок за модулем
- квадратичний
нелишок за модулем ![]() . Тобто, враховуючи критерій
Ейлера,
. Тобто, враховуючи критерій
Ейлера,
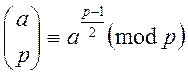 (2)
(2)
Критерій Ейлера дає одразу і формулу
обчислення символу Лежандра, але для великих ![]() обчислення
є досить складними. Наведемо властивості символу Лежандра, які значно спрощують
процес обчислення даного показника і, відповідно, визначення наявності
розв’язків (1).
обчислення
є досить складними. Наведемо властивості символу Лежандра, які значно спрощують
процес обчислення даного показника і, відповідно, визначення наявності
розв’язків (1).
Властивості символу Лежандра.
1. Якщо 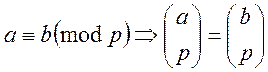
2. 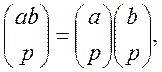 як наслідок:
як наслідок:
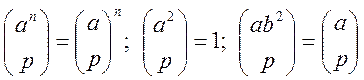
3. 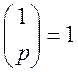
4. 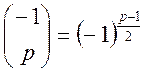 .
.
Якщо взяти до уваги, що для усіх простих чисел
![]() величина
величина 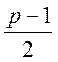 парна,
а для
парна,
а для ![]() , або
, або ![]() -
непарна, то дану властивість можна прокоментувати так: для всіх модулів типу
-
непарна, то дану властивість можна прокоментувати так: для всіх модулів типу ![]() число -1 є квадратичний лишок, а для
модулів типу
число -1 є квадратичний лишок, а для
модулів типу ![]() , або
, або ![]() -
квадратичний нелишок.
-
квадратичний нелишок.
Наприклад -1 за модулем 29 є квадратичний
лишок, бо ![]() , а для модуля 3 квадратичний нелишок, бо
, а для модуля 3 квадратичний нелишок, бо ![]()
Властивість 2 зводить обчислення символу
Лежандра ![]() за прости непарним модулем
за прости непарним модулем ![]() до обчислення символів
до обчислення символів 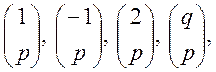 якщо
якщо ![]() -
просте непарне число.
-
просте непарне число.
5. 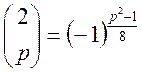
Якщо розглянути просте непарне число за модулем 8, то будемо мати для нього один з таких видів:
![]()
Якщо розглянути степінь 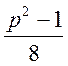 для цих видів, то будемо мати:
для цих видів, то будемо мати:
![]() :
: 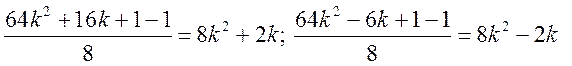 - парні степені
- парні степені
![]() :
: 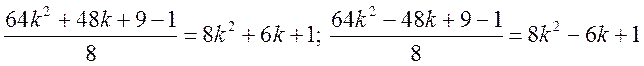 - непарні степені
- непарні степені
Тобто властивість 5. можна подати так:
Для чисел ![]() символ
Лежандра
символ
Лежандра 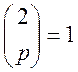 , 2 є лишком за модулем
, 2 є лишком за модулем ![]()
Для чисел ![]() символ
Лежандра
символ
Лежандра 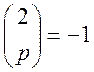 , 2 є нелишком за модулем
, 2 є нелишком за модулем ![]()
6. Закон взаємності двох простих непарних чисел:
Якщо ![]() та
та ![]() два різних непарних простих числа, то для
них виконується співвідношення:
два різних непарних простих числа, то для
них виконується співвідношення:
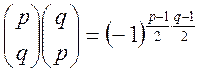
Число ![]() , як і
число
, як і
число ![]() подається за модулем 4 або як
подається за модулем 4 або як ![]() , або
, або ![]() . В
першому разі
. В
першому разі 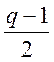 буде парним степенем, у другому
– непарним. Добуток степенів
буде парним степенем, у другому
– непарним. Добуток степенів 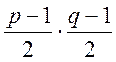 буде парним, якщо хоч
один із множників парний.
буде парним, якщо хоч
один із множників парний.
Отже, якщо хоча б одне
з чисел ![]() та
та ![]() має
вигляд
має
вигляд ![]() , то
, то 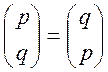 .
.
Якщо обидва числа
мають вигляд ![]() , то
, то 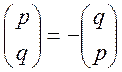
Приклади:
Розв’язання
Спочатку
спростимо конгруенцію: ![]() . Розкладемо
. Розкладемо ![]()
Для визначення наявності розв’язків обчислимо символ Лежанндра
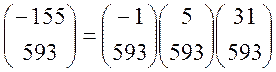
1) ![]() , тобто
, тобто 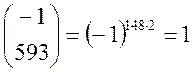 ,
,
2) 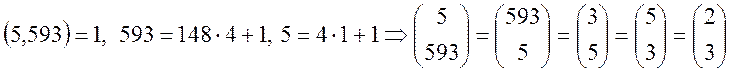 ,
, ![]() , отже
2 є нелишком по модулю 3,
, отже
2 є нелишком по модулю 3, 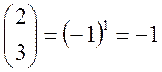
3) 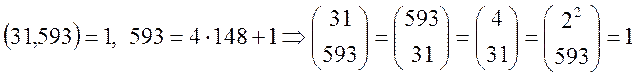
4) 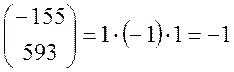
Висновок: Конгруенція ![]() розв’язків немає.
розв’язків немає.
Розв’язання
Спочатку
спростимо конгруенцію: ![]() . Розкладемо
. Розкладемо ![]()
Для визначення наявності розв’язків обчислимо символ Лежанндра
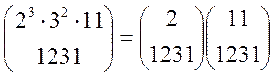
1) ![]() , тобто
, тобто 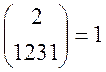
2) 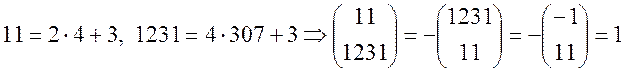
3) 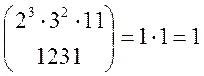
Висновок: Конгруенція ![]() має 2 розв’язки.
має 2 розв’язки.
Якобі узагальнив символ Лежандра на випадок,
коли модуль конгруенції ![]() є непарне число, яке
складене з простих чисел, тобто
є непарне число, яке
складене з простих чисел, тобто ![]() ,
, ![]() можуть повторюватися.
можуть повторюватися.
Означення:
Символом Якобі називається показник
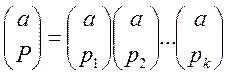 ,
,
де 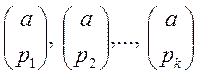 - є звичайні символи Лежандра.
- є звичайні символи Лежандра.
Нехай ![]() -
розкладання числа
-
розкладання числа ![]() на прості множники. Тоді за
властивостями символу Лежандра
на прості множники. Тоді за
властивостями символу Лежандра
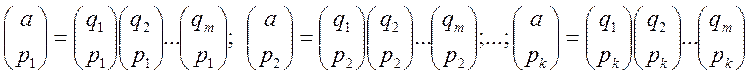 , тобто
, тобто
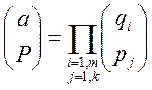
Теорема 1. Для символу Якобі вірні всі властивості 1-6 символу Лежандра.
Приклад. Обчислити:
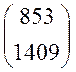
Розв’язання:
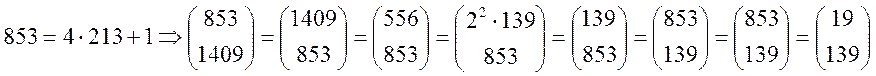
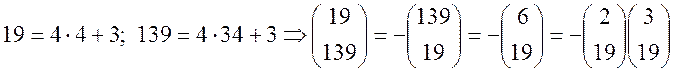
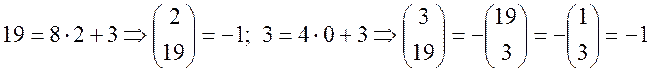
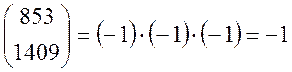
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.