Дані числа ![]() . Кожне з чисел, що є кратним
кожному з даних чисел, носить назву їхнього спільного кратного. Найменше
із усіх кратних називається найменшим спільним кратним даних чисел.
. Кожне з чисел, що є кратним
кожному з даних чисел, носить назву їхнього спільного кратного. Найменше
із усіх кратних називається найменшим спільним кратним даних чисел.
Нехай ![]() , тоді
, тоді ![]() і
і
![]() (властивості НСД, 2.) Нехай
(властивості НСД, 2.) Нехай ![]() - деяке кратне
- деяке кратне ![]() та
та ![]() , тобто
, тобто ![]() і
і 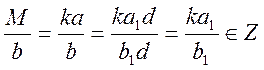 . Оскільки
. Оскільки ![]() , то
, то ![]() повинно ділитися на
повинно ділитися на ![]() , тобто
, тобто ![]() . Для СК
буде вірна формула:
. Для СК
буде вірна формула:
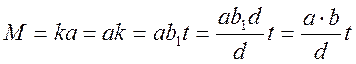
Найменше значення СК буде за умови, що ![]() , тобто
для НСК виконується формула:
, тобто
для НСК виконується формула:
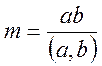 , тоді
, тоді ![]()
Теореми:
1.
Сукупність спільних
кратних чисел ![]() та
та ![]() співпадає
з сукупністю кратних для їх НСК.
співпадає
з сукупністю кратних для їх НСК.
2.
НСК ![]() та
та ![]() дорівнює
відношенню добутку цих чисел до їх НСД.
дорівнює
відношенню добутку цих чисел до їх НСД.
Вислови:
1. Число 1 має тільки один додатній дільник – самого себе. Одиниця стоїть осторонь у ряду натуральних чисел.
2. Найменший дільник, що не дорівнює 1, для будь якого цілого
числа є число просте. (Візьмемо число ![]() і його
найменший дільник
і його
найменший дільник ![]() . Допускаємо, що
. Допускаємо, що ![]() . Тоді
. Тоді ![]() ділиться
на
ділиться
на ![]() і на
і на ![]() , тобто
, тобто ![]() має дільник, менший за
має дільник, менший за ![]() , що є протиріччям вихідному посиланню.)
, що є протиріччям вихідному посиланню.)
3. Найменший дільник, що не дорівнює 1, для будь якого складеного
цілого числа ![]() не перевищує значення
не перевищує значення ![]() . (Нехай
. (Нехай ![]() .
Оскільки
.
Оскільки ![]() - найменший дільник, то
- найменший дільник, то ![]() . Отже
. Отже ![]() , або
, або ![]() .
.
4. Простих чисел безкінечно багато.
5. Решето Ератосфена для вибору простих чисел, які не перевищують даного числа N.
1)
обираємо перше просте
число – ![]() . Викреслюємо всі цілі числа з інтервалу
. Викреслюємо всі цілі числа з інтервалу ![]() , кратні 2.
, кратні 2.
2)
обираємо наступне найменше
просте число ![]() . Викреслюємо всі цілі числа з інтервалу
. Викреслюємо всі цілі числа з інтервалу ![]() , кратні 3.
, кратні 3.
3)
Повторюємо процес з
наступним ![]() .
.
4)
Обираючи чергове ![]() , звертаємо увагу на те, що кандидатів на
ви креслення слід розглядати з числа
, звертаємо увагу на те, що кандидатів на
ви креслення слід розглядати з числа ![]() , бо до цього числа всі
складені викреслені, як такі, що кратні простим числам, меншим за
, бо до цього числа всі
складені викреслені, як такі, що кратні простим числам, меншим за ![]() .
.
5)
Викреслення можна зупинити, коли ![]() перевищить
перевищить ![]() .
Усі кратні числа на той час будуть викреслені.
.
Усі кратні числа на той час будуть викреслені.
Базові вислови для складених чисел:
· Довільне ціле ![]() або
взаємо просте з даним простим числом
або
взаємо просте з даним простим числом ![]() , або ділиться на нього.
, або ділиться на нього.
· Якщо добуток декількох множників ділиться на
просте число ![]() , то хоча б один з множників теж ділиться
на
, то хоча б один з множників теж ділиться
на ![]() .
.
· Довільне ціле число можна розкласти на добуток простих множників єдиним способом. (враховуючи комутативність множення)
![]()
· У наведеному розкладанні деякі з множників
можуть повторюватися не один раз. Позначивши через ![]() тільки
різні множники, а через
тільки
різні множники, а через ![]() відповідні кратності
входження множників до числа
відповідні кратності
входження множників до числа ![]() , запишемо канонічне
розкладання довільного цілого числа
, запишемо канонічне
розкладання довільного цілого числа ![]() на
множники:
на
множники:
![]()
· Нехай ![]() -
канонічне розкладання довільного цілого числа
-
канонічне розкладання довільного цілого числа ![]() . Тоді
усі дільники цього числа можна подати у канонічному вигляді:
. Тоді
усі дільники цього числа можна подати у канонічному вигляді:
![]() , де
, де ![]()
· У відповідності до вищенаведеної формули,
кількість дільників ![]() довільного цілого числа
довільного цілого числа ![]() можна знайти так:
можна знайти так:
![]()
· Розглянемо канонічне розкладання ![]() довільних цілих:
довільних цілих:
![]() .
.
Тоді НСД цих чисел у канонічному вигляді прийме вигляд:
![]() ,
,
а НСК - ![]()
· Сукупність спільних дільників декількох цілих чисел співпадає з кількістю дільників їх НСД.
· НСК декількох взаємо простих чисел дорівнює їх добутку, а сукупність кратних декількох чисел співпадає з сукупністю кратних їх НСК.
Приклад:
Дані 2 числа 12348 та 867. Побудувати канонічну форму цих чисел, знайти їх НСД та НСК.
Розв’язання:
12348 за ознаками ділення ділиться на 4(22) і на 9 (32)
![]() - канонічне розкладання першого числа. Дільників
у першого числа буде
- канонічне розкладання першого числа. Дільників
у першого числа буде ![]()
![]() - канонічне розкладання другого числа.
Дільників у другого числа буде
- канонічне розкладання другого числа.
Дільників у другого числа буде ![]() - 17, 343 та 51
- 17, 343 та 51
НСД - ![]()
НСК - ![]()
Будь яке дійсне число ![]() можна подати, як
неперервний дріб. Нехай
можна подати, як
неперервний дріб. Нехай ![]() - найбільше ціле число,
- найбільше ціле число,
![]() . Тоді довільне неціле число
. Тоді довільне неціле число ![]() можна подати так:
можна подати так: 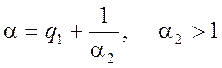 .
Відповідно,
.
Відповідно, ![]() , якщо вони не цілі, можна подати:
, якщо вони не цілі, можна подати:
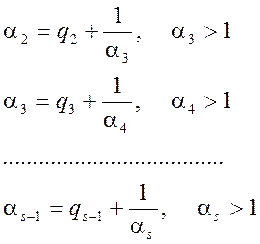 , або
, або 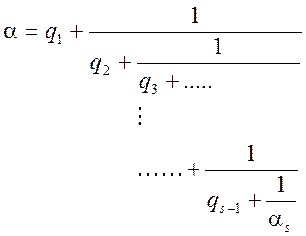
Якщо ![]() - ірраціональне число, то таке подання
буде безкінечним.
- ірраціональне число, то таке подання
буде безкінечним.
Якщо ж 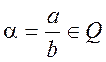 , то неперервний
дріб буде скінчений і розкладення можна отримати за допомогою алгоритму
Евкліда:
, то неперервний
дріб буде скінчений і розкладення можна отримати за допомогою алгоритму
Евкліда:
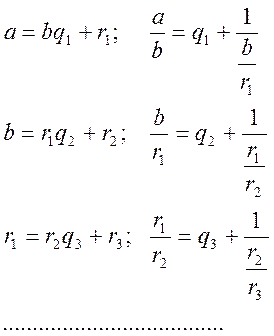
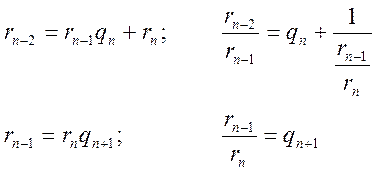 .
.
Тоді 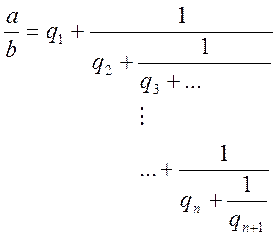
Зробимо позначення:
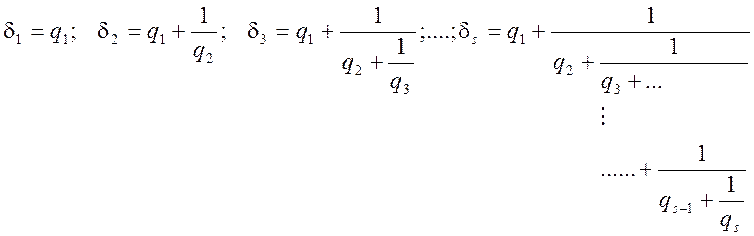
Такі дроби носять назву підходящих дробів
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.