Ліворуч у формулі стоїть сума усіх дільників числа ![]() . Позначимо цю суму
. Позначимо цю суму ![]() .
Праворуч у дужках маємо суми геометричних прогресій із знаменниками
.
Праворуч у дужках маємо суми геометричних прогресій із знаменниками ![]() . Використовуючи формулу суми геометричної
прогресії для
. Використовуючи формулу суми геометричної
прогресії для ![]() членів, отримаємо:
членів, отримаємо:
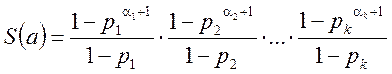 , або
, або
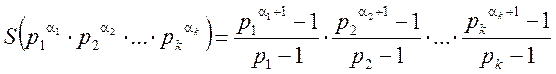
![]() - мультиплікативна
функція, для якої, за умови, що
- мультиплікативна
функція, для якої, за умови, що ![]() , сума дільників числа
, сума дільників числа ![]() дорівнює:
дорівнює:
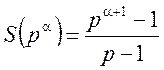
Приклад. Знайти суму дільників числа 1. ![]() ; 2.
; 2. ![]()
Розв’язання: 1. 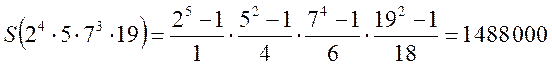 ;
;
2.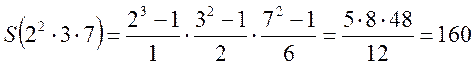 ,
,
Кількість чисел, менших за дане ![]() , взаємо простих з
, взаємо простих з ![]() .
Функція Ейлера.
.
Функція Ейлера.
Функція Ейлера визначає для довільного цілого додатного числа ![]() кількість чисел з ряду цілих
кількість чисел з ряду цілих ![]() , взаємо простих з числом
, взаємо простих з числом ![]() , тобто таких, що
, тобто таких, що ![]()
Позначається функція Ейлера: ![]()
Приклади: ![]() - за означенням.
- за означенням.
![]() - перед 2 є одне просте число – 1.
- перед 2 є одне просте число – 1.
![]() - взаємо прості з 3 – 1,2
- взаємо прості з 3 – 1,2
![]() - взаємо прості з 4 – 1,3
- взаємо прості з 4 – 1,3
![]() - взаємо прості з 5 – 1,2,3,4
- взаємо прості з 5 – 1,2,3,4
![]() - оскільки 13 – просте, то увесь ряд чисел
до цього числа є взаємо простий з ним.
- оскільки 13 – просте, то увесь ряд чисел
до цього числа є взаємо простий з ним.
Розглянемо канонічне подання довільного цілого ![]() .
Для довільного цілого функція Ейлера буде мати вигляд:
.
Для довільного цілого функція Ейлера буде мати вигляд:
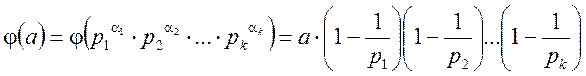 , або
, або
![]() , зокрема
, зокрема
1. для ![]() - простого числа -
- простого числа - ![]()
2. для ![]() - степені простого числа -
- степені простого числа - 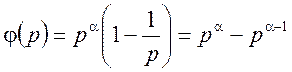
Функція Ейлера є мультиплікативною функцією.
Приклади:
![]()
![]()
Розглянемо ділення із залишком цілих чисел на деяке певне ціле число ![]() , яке будемо називати модулем. Подання
довільного цілого через неповну частку та залишок розглядалося в п. 1.1:
, яке будемо називати модулем. Подання
довільного цілого через неповну частку та залишок розглядалося в п. 1.1: ![]() . Серед множини цілих чисел, знайдуться
такі, які діленням на модуль
. Серед множини цілих чисел, знайдуться
такі, які діленням на модуль ![]() дадуть різні неповні
частки і однаковий залишок.
дадуть різні неповні
частки і однаковий залишок.
Наприклад, якщо за модуль узяти ![]() , то
можна навести ряд чисел, які діленням на 7 дають залишок 1:
, то
можна навести ряд чисел, які діленням на 7 дають залишок 1: ![]()
Числа, які від ділення на модуль ![]() дають
рівні залишки
дають
рівні залишки ![]() називаються рівно
залишковими, або конгруентними (порівнянними) за модулем
називаються рівно
залишковими, або конгруентними (порівнянними) за модулем ![]() .
.
Конгруенція чисел ![]() і
і ![]() за модулем
за модулем ![]() записується
так:
записується
так:
![]()
Такі твердження є еквівалентними з конгруенцією ![]() і
і
![]() :
:
1. ![]() - тобто
- тобто ![]() складає
конгруенцію із своїм залишком від ділення на модуль.
складає
конгруенцію із своїм залишком від ділення на модуль.
2. ![]()
Приклад: Розглянувши попередній приклад, можемо записати:
![]()
Ділення будь якого натурального числа можна подати двічі, наприклад:
![]() , або
, або ![]() , що
відповідає 2-м поданням через конгруенції:
, що
відповідає 2-м поданням через конгруенції:
![]()
Отже у загальному випадку будь яке число можна подати через конгруенцію так:
![]() або
або ![]()
І значить, поняття конгруенції можна подовжити на цілі від’ємні числа.
Тобто ![]()
Властивості конгруенцій:
· Для конгруенцій вірними є такі закони рівностей:
o рефлективність – ![]()
o симетричність – якщо ![]() , то
, то ![]()
o транзитивність – якщо ![]() ;
; ![]() , то
, то ![]()
· Інші властивості конгруенцій, які відповідають властивостям рівностей.
1. Конгруенції можна додавати:
![]()
Дійсно, ![]() .
Додамо дві рівності:
.
Додамо дві рівності:
![]() , отже
, отже ![]()
Властивість розповсюджується на довільну кількість порівнянь.
2. Доданок з будь якого боку конгруенції можна перенести у інший бік із зміною знаку:
![]()
Дійсно, розглядаючи за законом
рефлективності конгруенцію ![]() , додамо її до вихідної
, додамо її до вихідної
![]() , отримаємо
, отримаємо ![]()
3.
Оскільки ![]() , то до кожної з частин конгруенції можна
додати будь яке число, кратне модулю.
, то до кожної з частин конгруенції можна
додати будь яке число, кратне модулю.
![]()
4. Конгруенції можна перемножати:
![]()
![]()
Властивість розповсюджується на довільну кількість порівнянь.
5. Обидві частини конгруенції можна піднести до однієї і тієї ж степені:
Якщо ![]()
6.
Обидві частини конгруенції
можна помножити на однакове число ![]() .
.
Вірним є ![]() ,
отже за властивістю 5 маємо
,
отже за властивістю 5 маємо ![]()
7.
Узагальнення: Якщо у
виразі поліному від ![]() змінних із сталими коефіцієнтами
змінних із сталими коефіцієнтами
![]() замінити
замінити
![]() на
на ![]() ,
порівнянним
,
порівнянним ![]() за модулем
за модулем ![]() і
змінні
і
змінні ![]() замінити на порівняні з ними по модулю
замінити на порівняні з ними по модулю ![]() змінні
змінні ![]() , то
новий вираз поліному
, то
новий вираз поліному ![]() буде порівнянним з вихідним
виразом по модулю
буде порівнянним з вихідним
виразом по модулю ![]() .
.
![]()
Для доведення використовуються властивості 1-7.
Зокрема, для полінома ![]() -го степеня від однієї змінної:
-го степеня від однієї змінної:
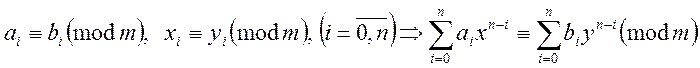
8.
Обидві частини конгруенції
можна поділити на спільний дільник ![]() , якщо
, якщо ![]() :
: 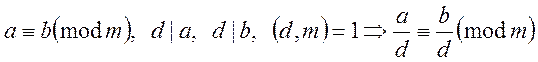
· Властивості, які належать тільки конгруенціям.
1. Обидві частини конгруенції і модуль можна помножити на одне й те саме число.
![]()
2.
Обидві частини конгруенції
і модуль можна розділити на будь який їх спільний множник ![]()
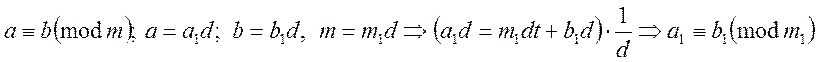
3.
Якщо ![]() та
та ![]() можуть бути конгруентними по декількох
модулях
можуть бути конгруентними по декількох
модулях ![]() , то конгруенція
, то конгруенція ![]() і
і
![]() вірна і за модулем, рівним НСК
вірна і за модулем, рівним НСК ![]() .
.
Оскільки ![]() ділиться на кожний з
модулів
ділиться на кожний з
модулів ![]() , то воно повинно ділитися і на НСК цих
модулів, тобто
, то воно повинно ділитися і на НСК цих
модулів, тобто ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.