Застосування теорії чисел в криптографії, страница 11

Підставимо в (4)  замість :

                                                                               (4*)

Оскільки модуль простий, значить хоча б один з множників повинен ділитися на модуль . Лінійні множники не діляться на модуль за допущенням доведення. Старший коефіцієнт конгруенції теж не ділиться на модуль, бо інакше степінь конгруенції був би нижчим. Отже приходимо до висновку, що конгруенція (4*) не можлива. Отже  не може бути коренем і не співпадати хоча б з одним значенням з набору .

Слід зауважити, що по-перше, ця теорема не підтверджує, взагалі, наявності розв'язків конгруенції -го степеня за простим модулем  і, по-друге, для складених модулів вона несправедлива, наприклад, у конгруенції першого степеня

 НСД . Отже, конгруенція має шістнадцять розв'язків.

Висновок. Конгруенція

 має більше ніж  розв'язків тоді і тільки тоді, коли вона тотожна, тобто коли всі її коефіцієнти діляться на.

Дійсно, якщо коефіцієнти даної конгруенції діляться на , то конгруенція виконується за будь-якого значення , тобто вона тотожна, число її розв'язків (що дорівнює ) буде більше ніж .

5.3 Конгруенції n-го степеня за складеним модулем.

Розглянемо конгруенцію

                                                    (1)

Якщо в конгруенції (1) , то конгруенція рівносильна системі:

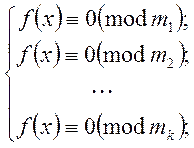
Якщо позначити через  кількість розв’язків ї конгруенції системи, то загальна кількість розв’язків вихідної конгруенції дорівнює:

Справедливість цієї теореми витікає з властивостей конгруенцій. Зокрема, якщо конгруенція виконується за модулем , то вона виконується і за будь яким дільником .

Приклад.

Розв’язати конгруенцію:

Розв’язання. , отже дана конгруенція відповідає системі:

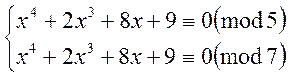
Після спрощення система буде мати вигляд:

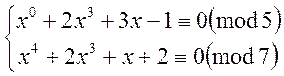
Перша конгруенція:

Розв’язки:

Друга конгруенція: . Шукаємо розв’язки серед повної системи абсолютно найменших лишків : 0, 1 – не розв’язки,  – розв’язок. Інші розв’язки шукаємо за схемою Горнера. Знайдемо ще два - .

Отже маємо 2 розв’язки у першій конгруенції і 3 розв’язки у другій. Загалом система, а отже і вихідна конгруенція має  розв’язків. Для того, щоб їх знайти необхідно розглянути 6 систем виду:

,

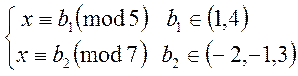Але ми можемо розв’язати дану систему у загальному вигляді і маючи її загальний розв’язок, підставити потрібні значення :

                                                                                      (*)

Підставимо  у друге рівняння системи:

.

Отже

Підставимо  до (*):, або

 - загальна формула розв’язку.

Залишилось тільки по черзі підставити у неї значення

Отже

Тепер розглянемо конгруенцію (1) в разі, якщо :

                                                                            (2)

Розв’язання такої конгруенції зводиться до розв’язання конгруенцій виду

                                                                                                     (3)

Розв’язання останньої конгруенції зводиться до розв’язання конгруенції

Для доведення цього факту нам необхідно буде згадати ряд Тейлора для розкладання полінома у околі точки :

.

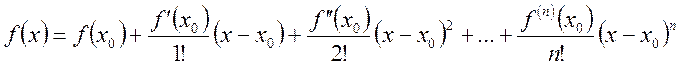Розглянемо конгруенцію (3). Її розв’язок , що еквівалентно запису

.                                                                          (**)

Підставимо це значення у конгруенцію

,

і розкладемо  у ряд Тейлора у околі точки :

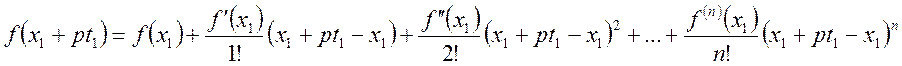, або

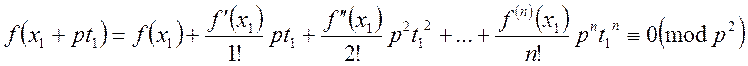
Відпросимо усі складові, кратні :

Оскільки  є розв’язком (3), то , отже конгруенцію можна скоротити:

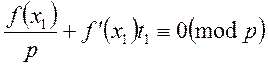, або 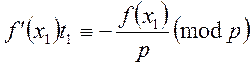. (Візьмемо випадок, коли  не ділиться на .)

Знайдемо розв’язок цієї конгруенції, позначимо його - . Отже . Підставимо значення  у (**):

. Якщо позначити , то будемо мати:

, або                                                                            (***)

Підставляємо його у конгруенцію

,

Розкладаємо за рядом Тейлора в околі , відкидаємо всі складові, кратні :

Зауважимо, що оскільки  не ділиться на , а  - ділиться. Скоротимо конгруенцію на . Будемо мати:

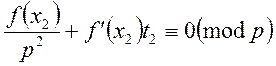. Розв’язок  підставимо до (***)

Продовжуючи таким чином, знайдемо кінець кінцем конгруенцію

, яка є розв’язком конгруенції (3).

Висновок: Будь який розв’язок  конгруенції  за умови, що  не ділиться на , дає єдиний розв’язок конгруенції (3).

Приклад.

Розв’язати конгруенцію

Розв’язання: