Застосування теорії чисел в криптографії, страница 8

c.  Використання підходящих дробів для розв’язку конгруенцій 1-го порядку.

Випадок , .

Розкладемо у неперервний дріб відношення 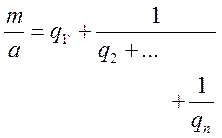. Будемо мати набір . За відомою схемою побудуємо підходящі дроби 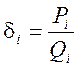. Розглянемо два останніх підходящих дроба: .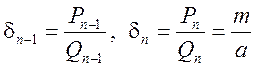

З властивостей підходящих дробів відомо: , отже . Враховуючи, що  ціле число, можна вважати за модульний період, який можна відкинути. Тобто маємо . Помножимо ліву і праву частину на число :

.

Отже, розв’язок конгруенції буде:

Приклад.

Розв’язати конгруенцію:

Розв’язання.

 - розв’язок єдиний. Розкладемо відношення  у неперервний дріб:

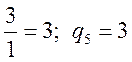
Будуємо схему:

і	0	1	2	3	4	5
		1	3	6	4	3
	1	1	4	25	104	337
	0	1	3	19	79	256

Із схеми маємо: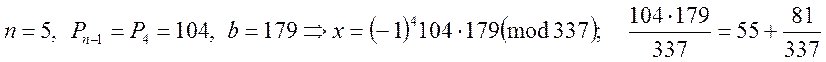

Отже,

d.  Розв’язання конгруенцій типу

 Обираючи  або  отримуємо . Чим більший степінь 2, ти краще. Нехай  найбільший степінь 2, такий, що . Якщо , маємо:

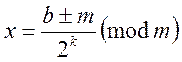
Якщо , скорочуємо конгруенцію на  та повторюємо процедуру для еквівалентної конгруенції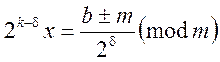

Приклад:

Розв’язати конгруенцію:

Розв’язання.

, отже можна вихідну конгруенцію подати так:

а)Обчислимо

                       

Обираємо . Найбільша степінь 2, яка ділить  є , отже переходимо до еквівалентної конгруенції:

б)

Обираємо , отже, еквівалентна конгруенція буде

в)

Обираємо , отже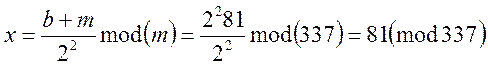

Відповідь:  - розв’язок співпадає з попереднім.

4.3 Обернений елемент за множенням.

Отримавши правила для розв’язання конгруенцій з одним невідомим, можемо дати відповідь на питання:

для яких елементів повної системи лишків за довільним модулем  існує обернений елемент з множення?

Щоб дати відповідь на це питання, треба розглянути розв’язання конгруенції

Виходячи з вимог існування розв’язку такої конгруенції – , бо права частина конгруенції дорівнює 1. Якщо за  взяти елементи повної системи залишків (як базу для всіх класів чисел за модулем ), то очевидно, що конгруенція не завжди буде мати розв’язок. Наприклад, . Отже, з повної системи треба відкинути всі елементи, кратні модулю. Отримаємо зведену систему лишків, кількістю  елементів. Для будь якого елементу зведеної системи за модулем  обернений елемент буде розв’язком конгруенції :

Позначимо обернений елемент через .

Отже для складеного модуля  обернений елемент існує тільки для його зведеної системи лишків і для будь якого елементу  з класу зведеної системи лишків дорівнює:

Якщо модуль є просте число , то зведена система лишків для нього співпадає з повною системою лишків.

Отже для будь якого елементу повної системи лишків за простим модулем  обернений елемент заданий та єдиний:

.

Висновки.

1. Повна система лишків за простим модулем  за операцією множення створює абелеву групу.

2. Повна система лишків за простим модулем  з заданими на ній операціями додавання і множення створює поле. Оскільки кількість елементів у повній системі лишків скінчена, то такі поля теж скінчені і носять назву полів Галуа.

4.4 Системи конгруенцій першого степеня з одним невідомим.

Розглянемо систему конгруенцій

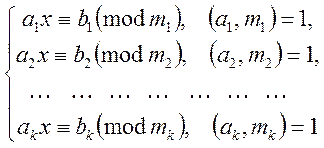                                                                             (1)

з одним невідомим за різними модулями. Будемо вважати також, що  - попарно прості.

Розв’язком системи конгруенцій з одним невідомим називається таке ціле число , яке задовольняє усі конгруенції даної системи.

По-перше, спростимо дану систему. Оскільки , то для  існує обернений елемент . Помноживши кожне рівняння системи на свій зворотній елемент, перейдемо до системи, еквівалентної даній:

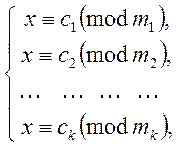                                                                                                    (2)

Отже, розв’язавши систему (1), ми тим самим знайдемо розв’язок системи (2).

Відповідь про існування та структуру розв’язку системи (2) дає

Китайська теорема про залишки:

Нехай дані  попарно простих чисел  та чисел , таких, що . Тоді існує таке єдине ціле число , у якого залишок від ділення на  становить  (тобто ).

Доведення.