Щоб скласти алгоритм обчислення будь якого підходящого дробу ![]() , позначимо
, позначимо ![]() та
та 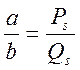 . Зауважимо, що у кожному підходящому дробу
. Зауважимо, що у кожному підходящому дробу
![]() достатньо
достатньо ![]() замінити
на
замінити
на 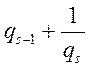 . Тоді
. Тоді
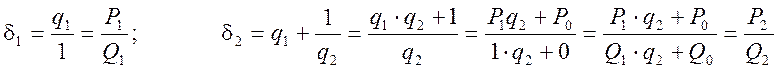
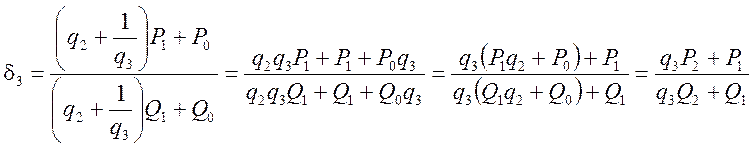
.................................................................................................................
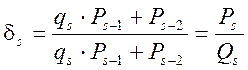
Отже, для обчислення будь якого ![]() нам
необхідно обчислити
нам
необхідно обчислити
![]() та
та
![]()
Для обчислення зручно застосувати схему:
|
і |
0 |
1 |
2 |
.... |
і-2 |
і-1 |
і |
... |
n-1 |
n |
|
|
|
|
.... |
|
|
|
.... |
|
|
|
|
|
1 |
|
|
.... |
|
|
|
.... |
|
|
|
|
0 |
1 |
|
.... |
|
|
|
.... |
|
|
Останні 2 рядки використовуються тільки у разі, коли дріб 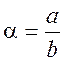 такий, що не скорочується.
такий, що не скорочується.
Приклад. Розкласти у неперервний дріб ![]() . Дріб такий, що не
скорочується. Розкладемо за алгоритмом Евкліда:
. Дріб такий, що не
скорочується. Розкладемо за алгоритмом Евкліда:
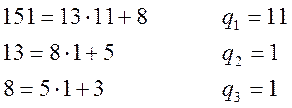
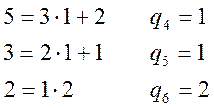 Отже,
Отже, 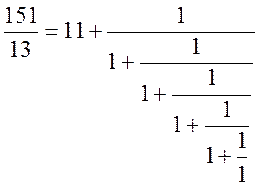
Наведена схема має вигляд:
|
і |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
11 |
1 |
1 |
1 |
1 |
2 |
|
|
|
1 |
11 |
12 |
23 |
35 |
58 |
151 |
|
|
0 |
1 |
1 |
2 |
3 |
5 |
13 |
Тобто дріб ![]() має такі підходящі дроби:
має такі підходящі дроби:
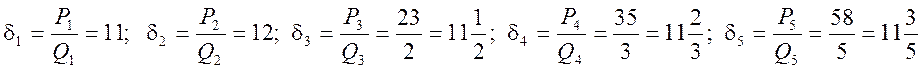 Якщо проаналізувати таблицю, то можна
помітити, що дане число розташовано між двома сусідніми підходящими дробами.
Якщо проаналізувати таблицю, то можна
помітити, що дане число розташовано між двома сусідніми підходящими дробами.
Властивості схеми розкладання:
1.
Для усіх ![]() маємо:
маємо: ![]() .
.
Дійсно, ![]()
![]() і т. д.
і т. д.
2.
Для усіх ![]() маємо
маємо 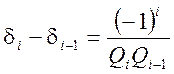
Дійсно, 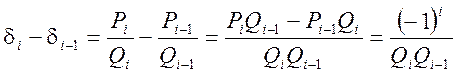
3. Для усіх ![]() раціональний
нескорочуваний дріб
раціональний
нескорочуваний дріб 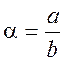 з додатнім знаменником завжди
розташований між
з додатнім знаменником завжди
розташований між ![]() та
та ![]() , ближче
до
, ближче
до ![]() .
.
1. Функція виділення цілої частини дійсного числа хповертає найбільше ціле число, яке не перевищує х:
![]()
Приклади: ![]()
2. Функція виділення дробової частини дійсного числа хповертає різницю між числом х та йогоцілою
частиною ![]() :
:
![]()
Приклади: ![]()
Приклад застосування функції виділення цілої частини:
Визначити степінь ![]() простого числа
простого числа ![]() , з яким це число входить до числа
, з яким це число входить до числа ![]() .
.
Розв’язання.
У числі ![]() множників, які кратні
множників, які кратні ![]() буде
буде ![]() . Серед
них множників, кратних
. Серед
них множників, кратних ![]() буде
буде 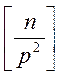 , і т.
д. доти, доки
, і т.
д. доти, доки ![]() , а
, а ![]() . Отже
загальна кількість входжень
. Отже
загальна кількість входжень ![]() до
до ![]() буде:
буде:
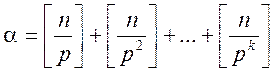
Приклад. Знайти з яким степенем число ![]() входить
до числа
входить
до числа ![]()
Розв’язання: 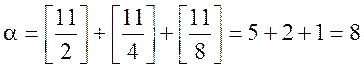
Дійсно, ![]()
Порахувавши усі степені 2, будемо мати: ![]()
Функція ![]() називається мультиплікативною,
якщо для неї виконуються 2 умови:
називається мультиплікативною,
якщо для неї виконуються 2 умови:
1. ![]() визначена для усіх
визначена для усіх ![]() і
хоча б для одного
і
хоча б для одного ![]() .
.
2. Для будь яких ![]() виконується:
виконується: ![]()
Приклад - ![]() , де
, де ![]()
Властивості мультиплікативних функцій.
1. Для будь якої мультиплікативної функції ![]()
Доведення: ![]()
Якщо розглянути ![]() попарно простих чисел,
то
попарно простих чисел,
то
![]() , зокрема
, зокрема
![]()
Наприклад, задамо мультиплікативну функцію так: ![]() .
Тоді для довільного цілого числа
.
Тоді для довільного цілого числа ![]() будемо мати:
будемо мати:
![]() , зокрема:
, зокрема:
![]()
2. Добуток двох мультиплікативних функцій – функція мультиплікативна:
Доведення:
![]() - задана функція.
- задана функція.
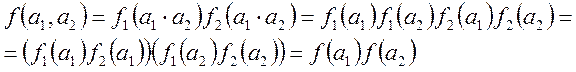
3. Нехай ![]() - довільне ціле число,
- довільне ціле число, ![]() - довільна мультиплікативна функція,
- довільна мультиплікативна функція, ![]() - множина усіх дільників
- множина усіх дільників ![]() виду
виду ![]() .
.
Тоді
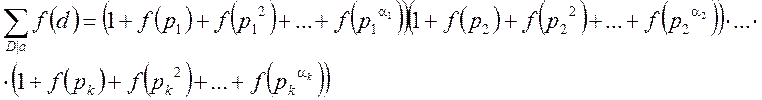
Доведення:
Для доведення необхідно перемножити усі дужки, отримаємо суму усіх дільників:
![]()
Приклади:
Кількість дільників числа ![]() .
.
Введемо мультиплікативну функцію ![]() .
Розглянемо для цієї функції 3-ю властивість мультиплікативних функцій:
.
Розглянемо для цієї функції 3-ю властивість мультиплікативних функцій:
Ліва частина: 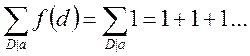 - кількість дільників
числа
- кількість дільників
числа ![]()
Права частина: ![]() ,
,
Отже, кількість дільників числа ![]() дорівнює
добутку степенів усіх простих чисел, що входять до канонічного розкладу числа,
збільшених на 1. Позначимо функцію визначення кількості дільників числа, як
дорівнює
добутку степенів усіх простих чисел, що входять до канонічного розкладу числа,
збільшених на 1. Позначимо функцію визначення кількості дільників числа, як ![]() . Тоді:
. Тоді:
![]()
![]() - мультиплікативна
функція, для якої кількість дільників числа
- мультиплікативна
функція, для якої кількість дільників числа ![]() , за умови, що
, за умови, що ![]() ,
, ![]() - просте число, дорівнює
- просте число, дорівнює
![]()
Приклад. Знайти кількість дільників числа 1. ![]() ;
2.
;
2. ![]()
Розв’язання: 1. ![]() ; 2.
; 2.![]() ,
,
Сума дільників числа ![]() :
:
Введемо мультиплікативну функцію ![]() і
підставимо її у властивість 3. Будемо мати:
і
підставимо її у властивість 3. Будемо мати:
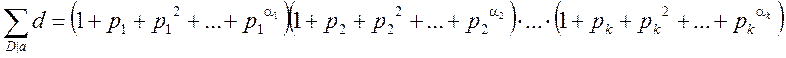
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.