Управление, основные понятия и определения. Классификация объектов управления. Основные свойства и характеристики объектов и систем. Исследование устойчивости нелинейных систем с помощью фазовых портретов. Абсолютный критерий Попова. Оптимальные системы АУ. САУ с эталонной моделью, страница 9

3) ответ: K₁оптим+ K₂оптим / P+ K₃оптим

графический метод определения настроек ПИД-рег-ра

1)исходные данные

1.1)мат описание объекта

1.2)мат описание рег-ра

2)методика определения коэф-ов

2.1)строится АФХ объекта в комплексной плоскости

2.2)к вершине каждого вектора восстанавливаем перпендикуляр на который откладываются отрезки, вычисляемые по ф-ле

А0=A()/Tu – K’Tu

Где  A()- длина вектора

Tu – время интегрирования

- частота

К’-промежуточный коэф-нт, для расчетов , который принимают равным 0.5

2.3)точки на отрезках, соответствующие одинаковому времени интегр-ия соединяют плавными кривыми.

2.4)из начала координат под углом 38градусов проводят луч и стоят касательные окружности таким образом, что бы они касались и луча и каждая своей кривой

2.5)из значений радиусов касательной окружности находят численные зн-ия коэф-ов К1 для разного зн-ия времени интегрир-ия  и строят область устойчивости

2.6)из начала координат области устойчивости сроят касательную и точка касания будет определять оптимальные значения К1оптим и Tu оптим

2.7)значения коэф-ов К2 находят по ф –ле       

3)ответ K₁⁰+K₂⁰/P+K₃⁰P

25.  Схемные методы улучшения качества регулирования

Если в случае одноконтурных систем управления не достигается требуемое качество (перерегулирование 20% или степень затухания 75%), то применяются более сложные системы управления: многоконтурные или каскадные. Чаще всего это необходимо для многоканальных или многосвязных объектов.

Для регулирования многосвязных объектов существуют так называемые системы компенсации, в которых одна из входных величин объекта воспринимается как возмущение.

Существует два возможных варианта таких систем:

1)  системы с компенсацией возмущения, когда есть возможность измерить это возмущение (например: температура, давление).

2)  системы компенсации по отклонению. Применяются, когда нет возможности непосредственно измерить возмущение, и оно допускается в объект (концентрация, рН, градиент, степень насыщения).

Физическая реализация подобных систем осуществляется на основе
принципа инвариантности: "Отклонение выходной координаты должно быть тождественно равно нулю при любых задающих или возмущающих воздействиях".

Полное выполнение принципа инвариантности возможно при двух условиях:

1   идеальная компенсация всех возмущающих воздействий F;

2   идеальное воспроизведение сигнала задания.

26.  Метод расчета 2-контурной системы для случая w внутр >> w внеш

Система компенсации по отклонению. Применяются, когда нет возможности непосредственно измерить возмущение, и оно допускается в объект (концентрация, рН, градиент, степень насыщения). Структурная схема имеет вид:

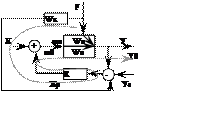
F – величина возмущения

Wо – передаточная функция объекта по основному каналу управления

Wк – передаточная функция динамического компенсатора

R – передаточная функция основного регулятора

Хр – управляющее воздействие

В данной системе рабочая частота по основному контуру регулирования должна быть больше рабочей частоты по каналу возмущения (ωо >> ωв).

1. Исходные данные

Структурная схема системы имеет вид:

1.1 Мат. описание ОУ W1 и W2

1.2 Задать типы управляющих устройств R1 и R2

1.3. w1 >> w2

2. Алгоритм расчёта

2.1 Принимая по внимание, что w1 >> w2 допускают, что сигнал z2 явл-ся пост-м для внутреннего контура (z2=const) и найстроки регулятора R1 рассчитывают любым известным методом, используя в качестве объекта W1

2.2 Находят настройки регулятора R2. Для этого его зрительно отсекают от исходной структруной схемы и преобразуют её от входного z2 к выходному y.

Любым известным методом рассчитывают настройки регулятора R2, используя в качестве объекта Wr2 экв.

2.3 Для проверки допущения, что z2 – const-a. Вновь находят настройки регулятора R1. Для этого его зрительно отсекают от схемы, которую преобразуют от входного x к выходному z1.

Любом известным методом рассчитывают настройки регулятора R1 используя в качестве объекта Wr1 экв.