2.9) К02 = 1/Tu0
3) ответ R1(p) = K01 +K02 /p
22. Д-регулятор
Пропорциональные рег-ры оказывают воздействие на объект когда рег-ая величина уже отклонилась от заданного значения. Интегральные рег-ры оказывают постепенное воздействие, наращивая его по интегральному закону, но ни тот ни другой не могут упреждать ожидаемое отклонение рег-ой величины. Поэтому был разработан Д-рег-ор математическая модель которого имеет вид:
Xp(t) =K3 dz(t)/dt где К3 – постоянная времени диф-ия
Он в начальный момент времени, когда П-регулятор оказывает слабое регулирующее воздействие, а И. не оказывает его вообще, оказывает влияние на объект, ликвидируя тем самым ожидаемое отклонение регулируемой величины при этом, чем больше возмущующее воздействие на объект, тем быстрее y будет отклоняться от заданного значения и тем существеннее д.б. влияние регулятора на объект.
Передаточная ф-ия Д-рег-ра имеет вид
R(p)=K3P
Реализация таких рег-ов в чистом виде физически невозможна, поэтому в их качестве используются реальные диф-ые звенья
R(p)=K3P/TP+1
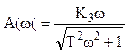
23. ПД-регулятор
- оказывает воздействие на объект пропорционально отклонению регулирующей величины и её скорости
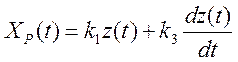
k3 – постоянная времени дифференцирования и опред-ет величину составляющей регулирующего воздействия по сторости
Структурно регулятор представляет собой параллельное соединение пропорционального и дифференциального регуляторов.
Передаточная функция и динамические характеристики
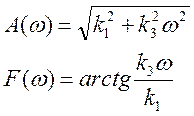
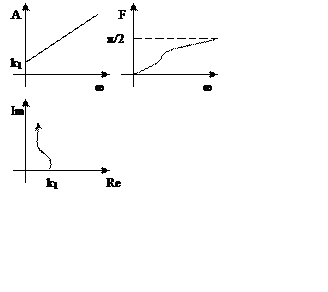
24. ПИД-регулятор. Аналитический метод. Графический метод
Воздействие на объект пропорционально отклонению рег-ой величины интегралу от этого отклонения и скорости изменения рег-ой величины.
Мат.модель
Xp(t)=
R(p)=K1+K2/P+K3P
A(
)=
F()=arctgK1/K2-K32
-
/2
Аналитический метод определения настроек ПИД рег-ра
1)исходные данные
1.1)мат. Описание объекта
1.2)мат. Описание рег-ра
1.3)критерий устойчивости Найквиста –Михайлова
1.4)среднеквадратичный критерий качества стремящийся к минимуму
1.5)степень колебательности которая выбирается m=0.221-если в физической реализации система имеет хоть одно пневматическое звено или m=0.75- если все звенья системы электрические
2)методика расчета
2.1)находится
расширенная хар-ка объекта путем искусственной замены 
делается
это для придания системе большей устойчивости, т.е. если расширенная система по
расчетам устойчива то исходная система тоже устойчива.
2.2)Из расширенной передаточной ф-ии объекта строиться расширенная АФХ объекта
2.3)из системы Ур-ий Н-М определяют АЧХ рег-ра и ФЧХ рег-ра
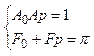
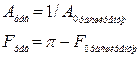
2.4)таким
образом для каждого значения выбранной частоты012
строиться вектор и АФХ рег-ра
2.5)Из вектора рег-ра находят так называемые параметрические ф-ии J и R гдеJ-мнимая параметрическая ф-ия, определяется как проекция вектора рег-ра на мнимую ось. R- реальная параметрическая ф-ия , на реальной оси
J=AрегsinFрег
R=AрегcosFрег
2.6)значение
мнимой реальной параметрической ф-ии для каждого зн-ия заносятся
в плоскость параметрических ф-ий
Это
экстремальная кривая максимум которой соответствует минимум
среднеквадратического критерия кач-ва и более кач-му процессу системы.
Найденные max и Jmax и Rmax
используются для дальнейших расчетов
2.7) Формируется система Ур-ий которая отражает св-ва только рег-ра на основании расширенной передаточной ф-ии ПИД рег-ра
R(p)=K1+K2/P+K3P
R=K1+K2/
+K3(
) | : (
)/(
)=
= K1-K3m- K2/(1+m2) + i[K3- K2/(1+m2)]
Система уравнений отражающая свойства регулятора и имеет вид
K3 max-
K2/max(1+m2)=Jmax
K1-K3mmax- K2m/max(1+m2)=Rmax
Алгоритм решения системы Ур-ий
1)задается любое значение К1
2)система Ур-ий решается относительно К2 и К3
3)составляется комплекс
0.25< К2К3/К12<0.75
При выполнении которого расчет считается законченным а найденные коэф-ты оптимальными если комплекс 0.75 то K1 уменьшают на 10% от предыдущего, если >0.75 то увеличивают
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.