Управление, основные понятия и определения. Классификация объектов управления. Основные свойства и характеристики объектов и систем. Исследование устойчивости нелинейных систем с помощью фазовых портретов. Абсолютный критерий Попова. Оптимальные системы АУ. САУ с эталонной моделью, страница 11

29.  Определение настроечных коэффициентов системы АУ с дополнительным импульсом от промежуточного параметра

Метод предназначен для расчета систем, частота вн. контура которых меньше частот внешнего.

Структ. схема им. вид:

где W_g – ПФ реального диф-го звена

Путем структурных преобразований диф. звено переносят через сумматор по ходу сигнала, добавляя обр. звено и схема приобретает вид классической двух контурной системы.

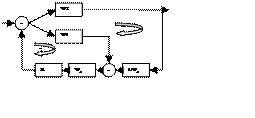
Переставляют w1 и w2 в зависимости от их поведения и расч. настр-ки рег-в R1 и R1 либо 1-м либо 2-м методом.

30.  Управление многосвязными объектами

Для многоканальных объектов, когда одна входная величина и несколько выходных, существуют каскадные системы управления, структурная схема которых, в общем виде, имеет вид:

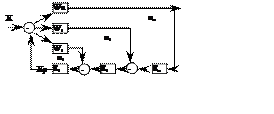
где: контур, крайний слева, называется основным или внутренним, контур, крайний справа – внешним, а все контуры между ними – промежуточными.

W – передаточные функции основного, промежуточных и внешнего объектов соответственно;

R – передаточные функции регуляторов основного, промежуточных и внешнего контуров соответственно;

ω – рабочие частоты основного, промежуточных и внешнего контуров соответственно.

Для подобных схем должно строго выполняться условие ω₁ > ω_i > ω_n , т.е. быстродействие внутреннего контура должно быть наибольшим, по сравнению с последующими, иначе система не реализуема физически.

Наибольшее распространение получили двухконтурные каскадные системы, поведение которых может быть описано двумя случаями:

1)  когда частота внутреннего контура намного больше частоты внешнего (различаются на порядок) ω₁ >> ω₂;

2)                    когда частоты внутреннего и внешнего контура соизмеримы.

31.  Схема компенсации с динамическими компенсаторами

Физическая реализация многоканальных систем осуществляется на основе принципа инвариантности: "Отклонение выходной координаты должно быть тождественно равно нулю при любых задающих или возмущающих воздействиях".

Полное выполнение принципа инвариантности возможно при двух условиях:

1   идеальная компенсация всех возмущающих воздействий F;

2   идеальное воспроизведение сигнала задания.

Реальные системы никогда не достигают принципа инвариантности и лишь довольствуются его частичной реализацией. Тем не менее, на основе принципа инвариантности выводятся формулы динамических компенсаторов Wк для первого (системы с компенсацией возмущения) и второго (системы компенсации по отклонению) случая.

(1)  Согласно принципам инвариантности выходная величина . Она складывается из

  

|=>

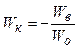
т.е. динамический компенсатор учитывает только свойства объекта.

(2) 

    

|=>

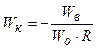
т.е. к характеристикам объекта прибавляются свойства регулятора

При физической реализации теоретических компенсаторов необходимо выполнение условий ("условия физической реализуемости динамических компенсаторов"):

1)  степень полинома числителя должна быть больше степени полинома знаменателя;

2)  степень чистого запаздывания по основному каналу регулирования должна быть меньше запаздывания по каналу возмущения.

На практике, передаточные функции динамических компенсаторов Wк выбирают из числа типовых звеньев, чьи характеристики наиболее близки к расчётным.

32. Особенности нелинейных САУ

Нелинейная система – система, содержащая хотя бы одно нелинейное звено, описываемое нелинейным уравнением.

В общем виде все нелинейные СУ можно разделить на 2 класса:

1.  оптимальные – статическая характеристика которых обладает обязательным экстремумом;

2.  релейные.

Все реально существующие системы являются нелинейными. Зачастую имеется возможность, ограничившись рассмотрением малых отклонений, свести задачу к исследованию линейной модели реальной системы, путём её модернизации.

Часто можно не учитывать, имеющиеся у какого-либо объекта, зону нечувствительности, если она достаточно мала по сравнению с установившимися отклонениями в системе, так же может быть отброшена петля Гистерезиса, если она достаточно узка.