Управление, основные понятия и определения. Классификация объектов управления. Основные свойства и характеристики объектов и систем. Исследование устойчивости нелинейных систем с помощью фазовых портретов. Абсолютный критерий Попова. Оптимальные системы АУ. САУ с эталонной моделью, страница 5

- единичный скачок;

- импульс;

- синусоида.

Снятие кривой разгона.

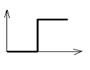Предусматривает подачу на вход объекта ступенчатого возмущения, путем энергичного изменения проходного сечения регулирующего органа. При этом отмечают величину и момент нанесения возмущения.

Величину изменения выходного параметра регистрируют до тех пор, пока он не примет нового установившегося значения (если объект устойчивый) или пока скорость изменения выходной величины не станет постоянной (если объект нейтральный). Кривые разгона обычно определяют на действующем объекте изменяя его входную величину на несколько % таким образом, что бы его реакция не выходила за пределы, ограниченные технологическим режимом..

Снятие импульсной характеристики

Предусматривает подачу на вход объекта импульсного возмущения в виде двух последовательных скачков, которые одинаковы по величине, но противоположны по направлению. Выходная величина при этом может принять тоже значение, что и до возмущения (если объект устойчивый) или какое то другое (если объект нейтральный).

Импульсную характеристику снимают в том случае, если ступенчатое возмущение приводит к нарушению нормальной работы объекта или к выходу регулируемой величины за заданные пределы. Если объект имеет несколько входных величин, то во время снятия временных характеристик по одному какому-либо каналу, необходимо все остальные каналы по возможности блокировать или установить постоянными.

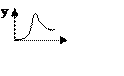
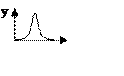По экспериментально полученной характеристике можно определить его математическую модель или передаточную функцию, а следовательно оценить его свойства.

14. Метод Ротача.

1) находится перегиб

2) в т.A строится касательная

n,k1,k2-взяты из таблицы ближайшее меньше к Tab/Tbd

Т=Тbd/к1

τ_у=Т*k₂

τ=Тав-τ_у

k=∆у/∆x

W_(p)=k*E^-τp/(Тp+1)ⁿ

Dx – величина входного скачка

15. Метод Симою.

Теорема: объект любой сложности может быть представлен как последовательность соединения диф-х неоднор. ур-ий 1-го порядка и передаточная функция которого будет иметь вид:

      (**)

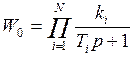
Z=A-Bt

          

Если объект состоит из нескольких апериодических звеньев, то выражение (**) будет описывать некоторую кривую.

Для нахождения  А и В  в хвостовой части графика (≈10%) строят касательную до пересечения с осью OZ.

a₁ – первая постоянная времени передаточной функции         

Чтобы решить, заканчивать расчёт или нет сравнивают две площади S₁ и S₂. Их соотношение не должно превышать 10%.

Если условие выполняется, то найденное Т₁ подставляют в передаточную функцию, в противном случае – находят значение постоянной времени Т₂, для чего строят кривую времени Z₁.

S1=(A*B)/2 – площадь под прямой у₁

S2=       - площадь под кривой Z(t)

((S1-S2)/S1)*100%

В общем виде передаточная функция имеет вид:

16. Метод Симою-2.

Служит для опр-я W(p) объекта либо к.-л. эл-та системы по его кривой разгона (метод площадей). В основе метода лежит представление о том, что объект может быть описан ЛДУ с пост коэф-ми.

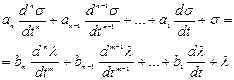
где a и b – const.

  - приведенная к 1 отклонение регулируемой величины в безразмерном виде.

  - приведенная к 1 возмущающее воздействие в безразмерном виде.

Послед. расчёта для объекта с самовырав. без транс.запазд.

Ось Х разбивает на отрезки интервалов ∆t исходя из условия, что на протяжении всего графика y(t) значения в пределах 2∆t мало отличаются от прямой.

Значения y(t) в конце каждого интервала ∆t делятся на ∆y(∞) и получившиеся значения b заносятся в таблицу.

t	s	1-s	q=t/F1	(1-q)	(1-s)(1-q)	1-2q+q2/2	(1-s)(1-2q+q2/2)
1	2	3	4
…	…	….	….		сум		сум

Послед. расчёта для объекта без самовырав. и транс.запазд.

А) tg a = (y2-y1)/dt = k1

Б) строится dy1 = k1*t

В) dy2 = dy1 – y(t)

Т.о. исходный объект условно разбивается на 2 фиктивных с соответствующими кривыми разгона dy1 dy2.