R(p)=k2*1/p , где k2 – интегральный настроечный коэффициент регулятора. k2 = 1/Ti
Мат. модель:
Предположим, что на вход регулятора поступил пост-й сигнал z=z0, тогда выходной сигнал будет опред-ся по формуле xp = z0Tp/Ti
По истечение времени Tp = Ti значения выходного сигнала: xp=z0, т.о. постоянная времени интегрирования равна времени в течение которого с момента поступления на вход регулятора постоянного сигнала, сигнал на выходе регулятора достигает значения равного значению сходного сигнала.
21. ПИ-регулятор. Аналитический метод. Графический метод
Применяется для комплексного использования достоинств пропорционального и интегрального регуляторов. Он оказывает воздействие на объект управления пропорционально отклонению и интегралу от отклонения регулируемой величины от заданного значения т.е. мат. модель регулятора имеет вид:
Xp(t)=k1z(t)+k2∫z(t)dt преобразуем по Лапласу получим R(p)=k1+k2 ⁄ p
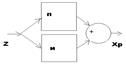Структурно ПИ регулятор представляет собой параллельное соединение
пропорционального и интегрального регуляторов. 
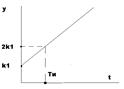
Второй рисунок – Переходный процесс ПИ регулятора: Ти-это время интегрирования Ти=1/k2
таким образом при отклонении регулируемой величины от заданного значения в результате срабатывает его пропорциональная часть а затем оказывается постепенное воздействие на объект под действием интегральной части.
 |
|||
 |
|||
Аналитический метод определения оптимальных настроек ПИ регулятора.
1) Исходные данные :
1.1) Мат. описание объекта
1.2) Мат. описание регулятора
1.3) Система устойчивости Найквиста –Михайлова
A0*Ap=1
F0+Fp=π
2) Методика определения:
2.1) Система преобразуется согласно исходным данным
A0(ω)*Ap(ω; k1; k2)=1 (*)
F0(ω)+Fp(ω; k1; k2)=π
a) Задаются любыми значениями частоты ωi и данная система ур-ий(*) решается относительно k1 и k2 . Пол ученные числовые значения в виде точки заносятся в систему координат которая наз-ся плоскостью настроечных коэффициентов
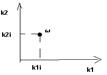
Максимум плоскости настроечных коэффициентов при этом соответствует min среднеквадратичного критерия качества
Б) Задается приращение ωi+Δω которое также подставляют в систему уравнений (*) и находят новые координаты плоскости настроек. Так продолжают до тех пор пока не будет найден перегиб или MAX плоскости настроек
2.2) MAX частоту используют для нахождения рабочей частоты ωраб=0.9ωmax либо 1.1ωmax
Выбор 0.9 или 1.1 осуществляют таким образом чтобы рабочая точка зрительнее находилась правее MAX.
2.3) Рабочую частоту подставляют в систему уравнений (*) и находят оптимальные значения k1 и k2.
3.)Ответ .
Графический метод определения оптимальных настроек ПИ регулятора.
1)Исходные данные
1.1)математическое описание объекта
1.2)мат-ое описание рег-ра
2)методика решения
2.1) строиться АФХ объекта
2.2) из вершины каждого вектора откладываются перпендикуляры
2.3)
на перпендикуляры откладывают отрезки 
A которые находят по формуле
A=Ai
)/Wi Tui где Tui - время интегрирования(выбирается произвольно)
2.4) точки с одинаковыми индексами время интегрирования соединяются плавными прямыми
2.5) из начала координат под углом 38градусов от отрицательной реальной оси проводят луч ОЕ
2.6) строят последовательно n- касательных окружностей (где n- число точек времени интегрирования или число кривых) таким образом что бы они касались, каждая своей кривой и луча ОЕ , все центры должны лежать при этом на отрицательной оси
2.7) найденные при этом радиусы R123 используются для определения пропорциональных коэф-ов
К11 =1/r1 К21=1/r2 К31 =1/r3
2.8) строят плоскость устойчивости в следующих координатах К1(Tu)
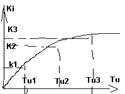
Все точки лежащие ниже этой прямой обеспечивают устойчивое управление. Для определения оптимальных параметров из начала координат строят касательную к этой плоскости. Такая касательная будет определять оптимальный К1 и Тu
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.