Примером существенных нелинейностей, которыми нельзя пренебрегать, являются релейные характеристики. Наиболее распространённые нелинейности имеют вид:

а. Звено с насыщением
б. Звено с зоной нечувствительности
в. Звено с мёртвым ходом
г. Идеальное двухпозиционное реле
д. Двухпозиционное реле с зоной нечувствительности
е. Идеальное трёхпозиционное реле
ж. Трёхпозиционное реле с зонами нечувствительности
з. Парабола.
В результате математического описания существующих систем составляется структурная схема, которая содержит линейные (т.е. линеализованные) и существенно нелинейных звеньев. При описании последних, в свою очередь, осуществляется идеализация с целью их упрощения до типовых нелинейностей.
33. Стационарный режим нелинейных САУ
Статические режимы нелинейных САУ определяются зависимостью статического значения входной величины от статического значения внешнего воздействия и имеют вид:
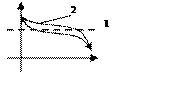
1 – для линейной
2 – для нелинейной
Статическая характеристика нелинейной СУ в целом строится по статическим характеристикам, составляющих её звеньев, исходя из их соединения которое определяется структурной схемой.
Построение производится графически, последовательность вывода та же, что и в линейных системах.
1. Последовательное соединение нелинейных звеньев

Задаются рядом значений входной величины xi, для каждого из этих значений находят соответствующее значение y1i.
По нему находится следующее значение y2i и т.д. по цепочке до нахождения всей цепочки.
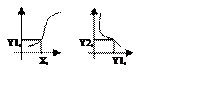
2. Параллельное соединение
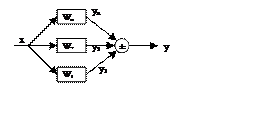
Ординаты искомой зависимости y(x) определяются как Σ ординат характеристик отдельных звеньев

3. Соединение с обратной связью
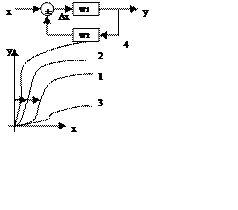
1 – Статическая характеристика звена W1, т.е. зависимость y=f(Δx)
2 – Зависимость xoc=f(g) т.е. Статическая характеристика звена W2
Из уравнения Δx=x± xoc находят x=Δx± xoc, где «-»соответствует положительной ОС, «+» - отрицательной.
Для каждого конкретного значения выходной величины «у» соответствующее значение «х» определяется по характеристикам 1 и 2.
Т.о. кривая 3 будет являться результирующей при отрицательной ОС, а кривая 4 при положительной, т.е. отрицательная связь уменьшает, а положительная увеличивает крутизну статической характеристики системы.
С помощью данных построений любая система может быть приведена к одноконтурной системе, состоящей из объекта и УУ, каждое из которых будет обладать своей статической характеристикой.
34. Динамика нелинейных систем
В линейных системах устойчивость и качество переходных процессов не зависит от величины внешних воздействий. Изменение величины возмущения вызывает в них только пропорциональное изменение выходной величины, не сказываясь на качестве переходного процесса.
Устойчивость линейных систем вообще не зависит от возмущения, если линейная система устойчива, то она устойчива при любых воздействиях.
В нелинейных системах качество процесса зависит от величины или вида внешнего воздействия, т.е. система устойчивая при одних возмущениях может быть неустойчивой при других.
Пр1.
Система устойчивая при малых воздействиях (кривая 1) м/б неустойчивой при больших, с получением апериодического (кривая 2) или колебательного (кривая 3) переходного процесса.
|

Такое возможно, если нелинейная часть системы содержит звено насыщения.
Пр2.
При малых воздействиях процесс носит расходящийся характер (кр 1), при увеличении внешнего воздействия колебания начинают сходиться(кр 2), установившимся режимом в этом случае будут незатухающие колебания (кр 3).

После любой попытки сбить незатухающе колебания к нулю будет возникать расходящийся процесс их восстановления (кр 1). Это вызвано наличием зоны нечувствительности нелинейного звена.
Т.е. у нелинейных систем существует ещё один вид установившегося переходного процесса – автоколебания.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.