Управление, основные понятия и определения. Классификация объектов управления. Основные свойства и характеристики объектов и систем. Исследование устойчивости нелинейных систем с помощью фазовых портретов. Абсолютный критерий Попова. Оптимальные системы АУ. САУ с эталонной моделью, страница 10

2.4 Принимая решение об окончании расчёта на основании нер-ва: di = (ki – ki / )/ki * 100% <= 10%

Ki – настройки регулятора R1 из 2.1

Ki / - из 2.3

При выполнении нер-ва расчёт заканчивают, в противном случае возвращаются в 2.2 и меняют настройки регулятора R2 в ту или иную сторону.

27.  Метод расчета 2-контурной системы для случая w внутр, w внеш соизмеримы

Система с компенсацией возмущения, когда есть возможность измерить это возмущение (например: температура, давление). Схема в этом случае имеет вид:

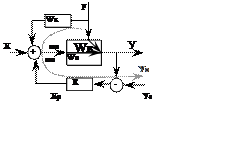
F – величина возмущения

Wо – передаточная функция объекта по основному каналу управления

Wк – передаточная функция динамического компенсатора

R – передаточная функция основного регулятора

Хр – управляющее воздействие

В данной системе рабочие частоты по каналу возмущения и основному каналу регулирования соизмеримы (ωо × ωв), т.е. их численные значения находятся в пределах одного порядка.

1. Исходные данные

1.1 Мат. модель объекта W1 и W2

1.2 Мат. модель регулятора R1 и R2

1.3 Частоты соизмеримые w1>=w2 (w немного больше – в пределах одного порядка)

2 Алгоритм расчёта

2.1 Расчёт параметров начинают с внешнего контура и принимают, что R1 = 1.

Эквивалентная передаточная ф-ция для расчёта R2 (по определению)

Wэкв = y1/z1

Учитывая, что w1 и w2 соизмеримы принимают допущение, что y1»z1, тогда Wэкв = y2/y1 = zW2/zW1 = W2/W1.

Используя любой известный метод находят настройки регулятора R2, используя в качестве объекта Wэкв.

2.2 Определяют настройки регулятора R1 для этого его зрительно отсекают от исходной схемы и преобразуя её от входного сигнала к выходному, находят передаточную функцию Wr1 экв = W2R2-W1.

Любым известным методом находят настройки регулятора R1.

2.3 Проверочный расчет

Вновь определяют настройки регулятора R2, но с учётом численных значений параметров регулятора R1. В качестве объекта исп-ют ф-му Wr2 экв = R1W2/(1+R1W1).

2.4 Принимают решение об окончании расчета на основании нер-ва: d < (ki – ki / )/ki * 100% <= 10%

Ki – настройки регулятора R2 из 2.1

Ki / - из 2.3

При выполнении нер-ва найденные коэффициенты считаются оптимальными и расчет заканчивают, в противном случае в 2.2 на 10% изменяют настройки регулятора R1.

28.  Метод расчета N-контурной системы АУ

1. Исх. данные:

1.1. Мат. модель n-мерного объекта управления

1.2. Мат модели n упр. устройств

1.3. Рабочая частота вн. контура д.б. > раб. частоты последующих контуров

w1>w2>…>wi>wn

2. Алгоритм расчета:

Структ. схема им. вид:

где х – вх. Параметр системы, у1, уi, yn – вых. параметры системы по каждому из регулируемых величин, W1, Wi, Wn – передаточные ф-ии объектов по каждому из контуров  управления, R1, Ri, Rn – ПФ-и упр-их устр-в в каждом контуре, z – управляющее воздействие.

2.1. расчет системы начинается с внешнего контура и опред. настр. парам-ры n-го упр-го устр-ва, для этого внешн. рег-р зрительно осекают от исх. структ. схемы и находят эквив. перед. ф-ю объекта.

где Wn – ПФ внешнего объекта управления.

2.2. Исп. получ. ПФ опр-т пар-ры внешнего рег-ра любым изв. методом.

2.3. Для нахождения настроечных коэф-в внешнего контура от исх. схемы зрительно отсекают вн. рег-р и в кач-ве объекта упр-я исп-т экв. ПФ

где Ri – ПФ упр-их устр-в пром-х контуров, кот. нах-ся по формуле R_i=W_i/W_i-1

2.4. Исп-я получ. ПФ экв. объекта, опред-т парам-ры внешнего рег-ра любым известным методом.

2.5. Для проверки результатов расчета вновь опред-т пар-ры внеш. контура с использованием данных внутр. упр-х устр-в. Для этого рег-р Rn рассчит-т вновь, исп-я в кач-ве объекта экв. ф-ю:

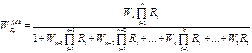
2.6. Рез-ты проверки должны удовл-ть усл-ю

где к_i’ и к_i’’ – настр. парам-ры внеш. упр. устр-ва, найден-е в п.п. 2.2. и 2.5 соотв.

Иначе коэф-ты рег-ра из п.2.4. изменяют на 10% и расчет повторяют из п. 2.5.