W(p) = W1(p) – W2(p)
Послед. расчёта для объекта cи транс.запазд.
a) t - время запаздывания, в течение которого функ. y от t=0 до t = t не превышает 0.001y(¥)
б) W(p) = W1(p)*W2(p)
W1(p)=exp(-p*t)
W2 – определяется из оставшейся части исходной кривой
17. Метод пассивного нахождения весовой характеристики объекта с помощью корреляционных функций.
Основаны на исследовании объекта в условиях его нормальной эксплуатации в течение длительного периода времени. Полученные данные обрабатываются с помощью мат. моделей, динамич. Хар-к
Корреляционная функция Кх(t) представляет собой зависимость 2-х случайных величин, удаленных друг от друга на значение времени t от времени. Чем меньше t, тем больше степень взаимодействия двух величин.
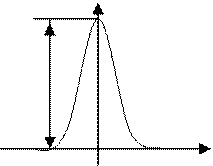
кх
s2х
t
Кх(j)=(1/N-j)*åх(i)*x(j+i) (1)
где N – число замеров или экспериментов,
j-текущий порядковый номер корреляционной функции,
i-порядковый номер замера
y(t)=òh(t)*x(t-t)dt h(t)-весовая хар-ка объекта
Численная формула определённая взаимной корреляционной функцией имеет вид:
Кxy(j)=(1/N-j)*å x(j)*y(t+j) (2)
в матричной форме уравнение (2) имеет вид:
Kxy = h(j) Kx(j) или весовая ф-ия h(j) = Кxy(j) Kx(j)-1 (3)
18. Типовые законы регулирования. Автоматические регуляторы.
Автоматический регулятор - это средство управления, получающее, усиливающее, преобразующее сигнал отклонения регулируемой величины от заданного значения и целенаправленно воздействующее на объект
 W- передаточная ф-ия объекта управления
W- передаточная ф-ия объекта управления
R- передат. ф-ия автоматического рег-ра
Y- выходная или рег-ая величина
Xp –рег-ая величина
Z- сигнал согласования
Автоматические регуляторы делятся на: линейные и нелинейные. К линейным относятся аналоговые, а именно (П, И, Д, ПИ, ПД и ПИД). К нелинейным (позиционные регуляторы)
19. П-регулятор. Аналитический метод. Графический метод
Передаточная ф-ия имеет вид R(p)=K1
где K1-коф-нт передачи рег-ра являющийся его параметром настройки
При K1=1 АФХ всей системы совпадает с АФХ объекта; при K1>1 АФХ системы приближается к точке (-1;0) а комплексной плоскости и следовательно к границе устойчивости. При K1<1 АФХ системы уходит от этой точки и от границы устойчивости, но слишком малая K1 вызывает потерю качества в системе.
Мат модель П-рег-ра имеет вид Xp(t)=К1Z(t) и следовательно в динамическом отношении П-рег-ор представляет собой усилительное звено, тогда АЧХ: А(ω)= K1 ФЧХ: F(ω)=0
Методы определения оптимального зн-ия настройки K1 П-рег-ра
Аналитический
1)исходные данные
1.1)мат. описание объекта
1.2)мат. описание рег-ра
1.3)критерий устойчивости Н-М
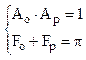
2)методика расчета
2.1)
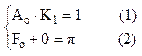
2.2)из уравнения (2) находим рабочую частоту как проекцию на ось ω в точке пересечения 2х графиков ФЧХ объекта и прямой на уровне π
 |
2.3) Рабочую частоту подставляют в формулу АЧХ объекта и находят рабочую амплитуду
2.4)
из Ур-я (1) находим формулу для опред численного значения коэффициента К1
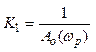
3) Ответ: R(p)=K1
Графический метод.
1.1 Мат описание объекта
1.2 Мат описание регулятора
Найти K1
2.) Расчет:
 2.1) Строим АФХ
2.1) Строим АФХ
2.2) в комплексной плоскости из начала координат под углом 380 к отрицательной реальной оси проводится луч “ОЕ”
2.3) Строят касательную окружность с центром на отрицательной реальной оси таким образом, чтобы она касалась и АФХ объекта и луча “ОЕ”
2.4)
коэф настройки находим по формуле ![]()
3) Ответ R(p)=K1
20. И-регулятор
Система управления с пропорциональным регулятором имеет установившуюся ошибку при регулировании, ликвидировать которую невозможно даже теоретически. Поэтому вводится интегральная составляющая, основная цель которой – ликвидация этой ошибки. Самостоятельно эти регуляторы не применяются из-за слишком медленного воздействия на объект и чаще всего исп-ся как составная часть более сложных регуляторов. Передаточная ф-ия интегрального регулятора имеет вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.