Устойчивые собственные колебания нелинейной системы называются – автоколебаниями.
В линейных системах автоколебания говорят о том, что система находится на грани устойчивости и является нежелательным переходным процессом.
Если же автоколебания возникли в нелинейной системе, то это не означает, что она непригодна к эксплуатации т.к. во-первых, эти колебания м/б настолько малы по амплитуде, что не будут оказывать заметного влияния на работу системы. Во-вторых, в системе в принципе возможны автоколебания с большой амплитудой, но для того чтобы они возникли, необходимы такие большие воздействия, которые не могут возникнуть при нормальной эксплуатации системы.
Однако для уменьшения амплитуд автоколебаний существует несколько структурных методов:
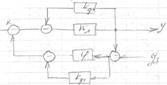
1 – размещение фильтрующего элемента перед нелинейным звеном
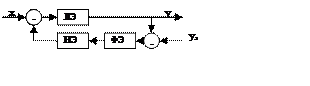
В качестве фильтра м/б использованы: ПИ-регулятор, апериодическое звено и реальное дифференциальное звено.
2 – Охват нелинейного элемента отрицательной обратной связью.
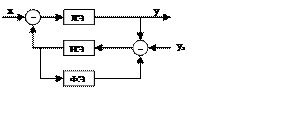
Фильтр – апериодическое звено.
3 – Охват и линейного и нелинейного элементов внутренней обратной связью с дифференциальной составляющей.

35. Исследование устойчивости нелинейных систем с помощью фазовых портретов
Типовой набор фазовых портретов базируется на мат модели колебательного звена.
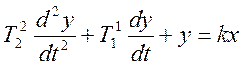
Решением ДУ 2-го порядка является выражение вида
![]()
В зависимости от поведения коэффициентов α и ω возможны следующие типы фазовых портретов
1- α<0 ω=0 y=Ae-αt ỷ=-Aαe-αt
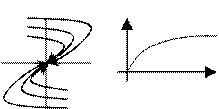
Устойчивое апериодическое звено
2- α>0 ω=0 y=Ae-αt ỷ=-Aαe-αt
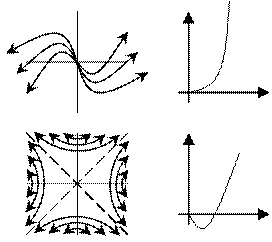
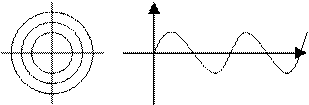
3- α=0 ω≠0 y=Acos ωt ỷ=-Asin ωt - ω
Фазовый портрет системы находится на границе устойчивости, в следствие того, что её характеристическое уравнение имеет пару сопряжённых мнимых корней.
Здесь каждому начальному отклонению от установившегося значения соответствует своя амплитуда незатухающих колебаний
37. Абсолютный критерий Попова.
Относится к системам вида:
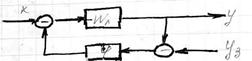
![]() - перед. ф-ция линейной части системы;
- перед. ф-ция линейной части системы; ![]() - перед. ф-ция нелинейной части системы.
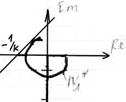
Для определения устойчивости нах-ся частотная хар-ка линейной части системы:
- перед. ф-ция нелинейной части системы.
Для определения устойчивости нах-ся частотная хар-ка линейной части системы: ![]() её получачают из АФХ линейной части путём
умножения ординат последней на текущее значение частоты. Возможны 2 варианта
поведения системы: 1) Предположим, что линейная часть системы явл. устойчивой,
тогда критерий закл в сл: система явл абс уст, если при устойчивой линейной
части через точку
её получачают из АФХ линейной части путём
умножения ординат последней на текущее значение частоты. Возможны 2 варианта
поведения системы: 1) Предположим, что линейная часть системы явл. устойчивой,
тогда критерий закл в сл: система явл абс уст, если при устойчивой линейной
части через точку ![]() можно провести хотя бы 1 прямую,
которая не пересекала бы функцию
можно провести хотя бы 1 прямую,
которая не пересекала бы функцию ![]() . 2) Предположим,
что линейная часть не уст, то исходная структурная схема преобр. сл. образом: В
систему вводятся 2 фиктивных звена с коэфф передачи. В рез-те получается
система, состоящая из линейной части системы с перед функцией
. 2) Предположим,
что линейная часть не уст, то исходная структурная схема преобр. сл. образом: В
систему вводятся 2 фиктивных звена с коэфф передачи. В рез-те получается
система, состоящая из линейной части системы с перед функцией ![]() и нелинейной частью с передаточной ф-цией
и нелинейной частью с передаточной ф-цией ![]() . Система называется абс. устойчивой,
если через точку
. Система называется абс. устойчивой,
если через точку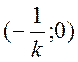 можно провести хотя бы 1 прямую,
которая находилась бы слева от хар-ки
можно провести хотя бы 1 прямую,
которая находилась бы слева от хар-ки ![]() .
.
38. Оптимальные системы АУ.
Постановка
задачи и её решение включают в себя несколько этапов: 1) Выбор и обоснование
цели оптимизации; 2) согласование цели с имеющимися возможностями; 3)
реализация способа достижения цели с учетом имеющихся ограничений. Существуют
объекты, для которых нет мат.описания и с учетом малого объема информации их
называют черным ящиком. При постановке оптимизации вводится понятие совокупности
данных (D), которое
необходимо для оптимизации объекта или системы. Совокупность данных включает в
себя сувокупность условий (Q), совокупность оптимизируемых параметров (X), совокупность показателей качества (y), совокупность ограничений (O). Следует различать локальные и глобальные
экстремумы. Для объекта с одним варьируемым параметром ф-ция качества
представляет собой ф-цию одной переменной. Она может иметь несколько локальных
экстремумов и только один глобальный. Для двухпараметрических объектов ф-ция
качества явл поверхностью сложной формы, а для многопараметрических
объектов гиперповерхностю. Условию одноэкстремности соотв-ют выпуклые
функции, основное условие которых: любая секущая пересекает её не более чем
в 2 местах. Методы мат.программирования: линейная, геометрическая,
выпуклая, нелинейная и стохастическая. В зависимости от вида и объема
используемой информации алгоритмы управления бывают: 1) алгоритмы управления,
основанные на обработке данных нормального функционирования объекта; 2) ау, исп
всю текущую информацию и часть априорной (адаптивные системы); 3)ау на основе
применения эталонных матем-х моделей исп-ют всю текущую и всю априорную инф. об
объекте. Работоспособность алгоритма – отношение потерь, кот образуются
при применении этого алгоритма к потерям, образующимся в режиме жесткой
стабилизации. 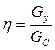 . Если n<1 – алгоритм
работоспособный и целесообразный, n=1 – работоспособный но не цел., n>1
– неработоспособный.
. Если n<1 – алгоритм
работоспособный и целесообразный, n=1 – работоспособный но не цел., n>1
– неработоспособный.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.