3 Теоретические сведения
3.1 Построение системы нечеткой логики
Такая система строится для каждого варианта задания по аналогии с выполнением лабораторной работы 2 в модуле FuzzyLogic системы Matlab. В каждом варианте устанавливается необходимое число входов, самостоятельно выбираются диапазоны изменения входных и выходной переменных, тип и количество функций принадлежности для каждой переменной, формируется соответствующая варианту база знаний. Результат (риск системы) проверяется при моделировании работы созданной системы через меню View –Rules.
Моделирование входных переменных
При моделировании используется метод обратной функции, сущность которого заключается в том, что по функции распределения (ФР) входной переменной путем розыгрыша находится значение этого признака. На рис.1 показаны графики плотности вероятности (ПВ, слева) и ФР (справа) некоторой величины, подчиняющейся нормальному закону.
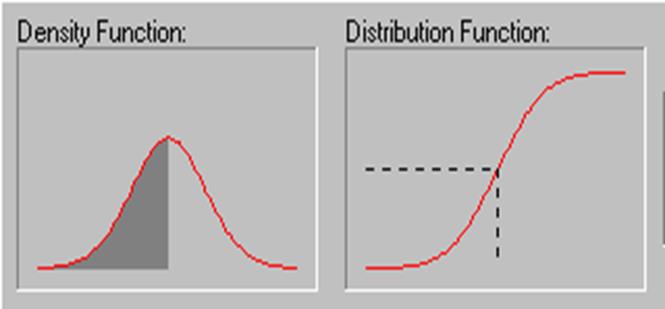
Рисунок 1 - Графики плотности вероятности (слева) и функции распределения (справа)
Как известно из теории вероятности, вся площадь под кривой ПВ равна единице, а ФР определяется как накопленная сумма (интеграл) от ПВ, поэтому на правой границе диапазона изменения переменной ФР асимптотически стремится к единице. На рис.1 показана ситуация, когда заштрихованная область под кривой ПВ равна приблизительно 0,5, т.е. вероятность в этом случае составляет 50%. На графике ФР (справа) эта же вероятность отложена на вертикальной оси, а определенное при этом значение аргумента совпадает с аргументом на горизонтальной оси левого графика. Ось ординат ФР (правого графика) имеет диапазон от 0 до 1 (100%), поскольку определяет собой вероятность любого события. Вследствие этого для моделирования надо взять любое случайное число из интервала [0,1] и отложить его на вертикальной оси, далее следует из этой точки провести горизонтальную линию до пересечения с кривой ФР, а из точки пересечения опустить перпендикуляр на горизонтальную ось. Таким образом, на этой оси получаем первое разыгранное значение некоторого признака. В этом заключается сущность метода обратной функции.
Для получения случайного числа из интервала [0,1] на заре развития этого метода использовалась рулетка, откуда появилось название (метод Монте-Карло). Разыграв определенное количество случайных чисел (разумеется, уже не с помощью рулетки), получим то же количество значений моделируемого признака. Подобная процедура повторяется для всех разыгрываемых переменных, и в итоге получаем таблицу смоделированных значений, состоящую из n строк (количество розыгрышей) и m столбцов (число переменных).
Уравнение регрессии
Смоделированные значения входных переменных (п.2) используются для определения величины риска через систему нечеткого вывода, полученного для данного варианта в п.1. Итогом этой процедуры является таблица, отличающая от предыдущей только наличием еще одного столбца, в котором приведены найденные значения риска. Эти данные применяются для нахождения уравнения регрессии, связывающего выходной параметр - риск - со всеми входными переменными.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.