Представление исходных данных. Визуализация многомерных данных в среде Statistica (Лабораторная работа № 1), страница 15

1. Рассмотрим    задачу,  сходную  с  рассмотренной  выше,  т.е.  в  момент  времени  0  портфель содержит  акции  компаний  А,  В  и  С,  котирующиеся  в долларах  США.   Требуется  вычислить  однодневный  90%  VaR  в  евро,    который  можно  записать  как        1-day  90%   EURVaR.   Здесь  базисная  валюта  отличается  от той,  в  которой  котируются  активы.  Вследствие  этого  исходные  данные,  использованные  в  линейном способе  расчета,  изменятся  за  счет  добавления  еще  одного  столбца,  который  отражает  изменение  обменного  курса  между  долларом  и  евро  на  протяжении  21  торгового  дня.  Таким  образом,  начальные   данные   принимают  вид, показанный  в табл.6. 

                       Таблица 6 – Исходные  данные

43,93	79,52	13,8	0,85
44,05	78,59	14,05	0,8525
44,66	79,6	14,45	0,8589
45,24	79,4	14,3	0,8442
45,21	79,51	14,2	0,8547
44,89	79,82	13,89	0,8537
45,68	79,23	14,43	0,8565
45,6	79,58	14,87	0,8511
45,73	79,05	14,73	0,8499
45,6	80,14	14,7	0,8425
46,22	81,4	15	0,8458
46,5	81,24	14,78	0,8486
46	82,42	14,8	0,8552
45,6	80,15	14,55	0,8534
45,61	79,61	15,12	0,8616
44,35	78,86	14,75	0,8651
44,43	79,44	15,03	0,8688
44,36	78,31	14,93	0,8674
44,82	78,58	15,25	0,8752
43,6	78,4	14,9	0,8747
43,76	78,62	15,04	0,8687

Портфель имеет  следующую  структуру:

·  20000 акций  компании  А;

·  -10000  акций  компании  В (короткая  позиция);

·  35000  акций компании  С.

Эту  структуру  можно  представить  в  виде  вектора –строки:

h = (20000  -10000  35000).

Ключевой  вектор  К¹  в  данном случае  имеет  вид

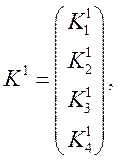
где   К¹_j   -  стоимость одной   акций  компаний    в  момент  времени  1  в  USD;  К¹₄  -  обменный   курс  USD/EUR.

          Примем,  что  функция  стоимости портфеля   является   квадратичной  и  имеет  вид:

Будем  считать,  что  ключевой  вектор  К¹  распределен  по многомерному  нормальному    закону  со  средним   значением,  равным                          .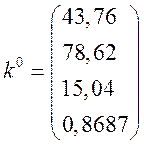

          Для  оценки  ковариационной матрицы  поступим,  как  и  выше,  т.е.  выполним  следующие  шаги:

·  скопируем  данные  таблицы  6  в  пакет Statgraphics;

·    вычислим  ковариационную матрицу  в  этом  пакете  аналогично  предыдущему случаю;

·  результат  вычисления  ковариационной матрицы  показан  в  табл. 7.

Таблица 7 -  Ковариационная  матрица

·  округлим  полученные  результаты  и  сведем  их  в  табл. 8

Таблица 8   -  Округленные  значения  ковариаций

          На   диагонали матрицы  находятся  дисперсии  стоимости  трех  видов  акций  и  коэффициентов  пересчета  доллара и  евро.  Соответствующие  среднеквадратические  отклонения  (СКО),  равные  корню  квадратному  из  дисперсий,  определяются  как

  σ₁ = 0,843;     σ₂=1,039;      σ₃=0,412;    σ₄= 0,0097.

          Таким  образом,  установили  параметры  многомерного  закона  распределения  ключевого  вектора:  среднего значения  и  ковариационной  матрицы.