Представление исходных данных. Визуализация многомерных данных в среде Statistica (Лабораторная работа № 1), страница 23

Возраст (год)	Доход (долл)	Квартира (балл)	Класс
34 34 37 37 36 36 37 25 43 34 16 24 24 25 25 22 22 22 19 19	1005 1058 1224 1117 1056 1092 868 933 937 948 198 196 251 216 222 196 223 169 200 233	7 10 11 13 11 11 8 9 7 15 2 4 2 4 4 4 5 3 5 4	1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2

Выполнить  следующие  действия:

1.  Создать новый  файл  в пакете  SNN,  нажав  File – New -  Network(Файл – Новый – Сеть),  после чего   в окне   CreateNetwork(Создать  сеть)  указать нужное количество входов  (3)  и выходов (1).

2.  Скопировать  данные  варианта 1  в  созданный  файл,  предварительно  дополнив  его 19 строками.

3.  Разделить  выборку  из 20  строк  на обучающую  и контрольную  по  10  строк  каждая,  после чего  перемешать все  строки.  

4.  Создать  сеть  в  виде  трехслойного  персептрона для  распознавания  субъектов  (физических  лиц)  на  два  класса.

5.   Обучить  сеть  методом  обратного распространения ошибки.   

6.  Убедиться  в  работоспособности  сети,  предъявляя  на  ее  вход   субъекты  разных  классов  (как использованные  при  обучении,  так и  совсем   новые).

7.  По таблице «Статистики  классификации» оценить  доли  перепутанных  классов.

8.  Обработать  данные посредством  интеллектуального  решателя.

Вариант  2. Классификация  предприятий  на  группы  «стабильных»  и  «нестабильных».  Риск  оценивается  как  доля  «перепутанных»  классов.

1.  Примем,  что  каждое  предприятие  характеризуется  набором  из  3  признаков.

Для  стабильных  фирм  средние значения  и  СКО  для  3 признаков  составят:  100; 10    50; 5    1000; 100.

Для  нестабильных  фирм  средние значения  и  СКО  для  3 признаков  составят:  10; 1    5; 1      100; 10.

2.  Смоделировать  для  каждого  предприятия  по  20    значений  признаков с  помощью  пакета Statistica:

·  Открыть  новый  файл,  состоящий  из 20 строк  и  6  столбцов  (рис.1).

Рисунок  1 -  Новый файл в  пакете  Statistica

·  Через  меню  Data – VariableSpecs… вызвать  окно  определения  переменной,  в  нижней  части  окна  написать  формулу  =vnormal(rnd(1);100;10),  учесть  тип переменной  присвоив  им тип  Integer  (целые и после   нажатия  ОК  в  первом столбце  появятся  20 чисел,  представляющих  смоделированные  значения  первого  признака  для  предприятий  первого  класса.  Данная  процедура  является  моделированием  методом  Монте-Карло  значений  нормально распределенных  величин  по  среднему  и СКО. 

·   Повторить  эту   процедуру  для  всех  6 параметров,  памятуя о том,  что  при  каждом  розыгрыше  в  формулу   подставляются   разные  величины  среднего  и  СКО.

 3.Открыть  пакет  StatisticaNN,  создать  в  нем  новый  файл  размерностью  40 строк,  4  столбца  и  скопировать  в  него  все  разыгранные  значения  параметров  предприятий. Копирование должно  осуществляться  таким  образом,  что  в  первые 3  столбца  вначале  вводятся  первые  20  строк   первых  3  столбцов  разыгранных значений   параметров  «хороших»  предприятий.  Затем  в  эти  же  столбцы ниже   вводятся  20  строк  с  разыгранными  значениями  4,  5  и  6  столбцов   из  таблицы  в  пакете   Statistica(«плохие»  предпрятия).    

  Четвертый  столбец  здесь  определяет  номер  класса  и  состоит  из  20  единиц  и  20  двоек,  соответственно. Результат  этих   действий  -  на рис.2.  (Естественно,  что  разыгранные  данные  будут отличаться от приведенных в  таблице  рис.2). (Естественно,  что  разыгранные  данные  будут отличаться от приведенных в  та,  после чего  перемешать все  строки.

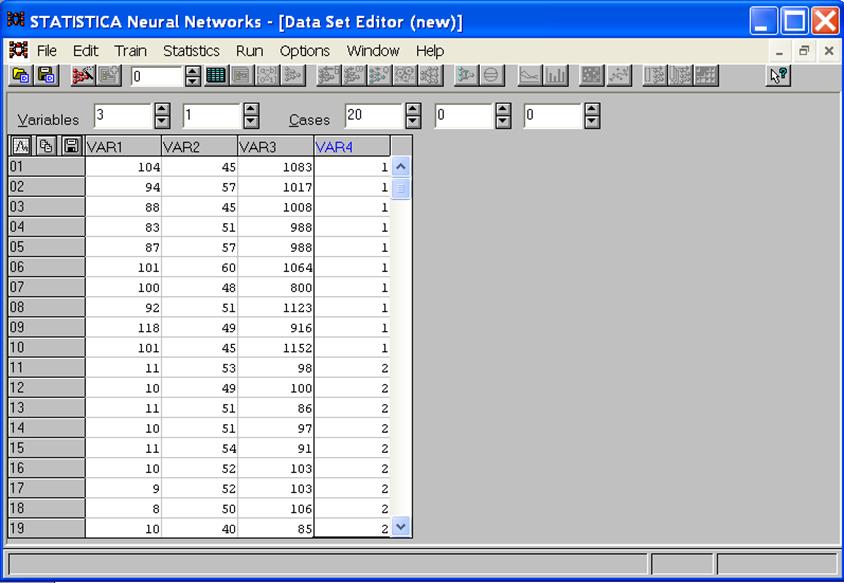
Рисунок  2  -  Перенесенные  в  пакет  SNN  разыгранные  данные

4. Создать и  обучить  сеть  на  распознавание  двух  классов.

5.  По таблице «Статистики  классификации» оценить  доли  перепутанных  классов.

6.  Убедиться  в  работоспособности  сети,  предъявляя  на  ее  вход   объекты  разных  классов  (как обученных,  так и  совсем   новых).

7.  Обработать  данные посредством  интеллектуального  решателя.