Представление исходных данных. Визуализация многомерных данных в среде Statistica (Лабораторная работа № 1), страница 5

Главная  идея  нечеткой логики  (FuzzyLogic) состоит  в  том, что    интеллектуальный  способ  рассуждений,  опирающийся  на  естественный  язык  общения  человека,  не  может  быть  описан  в  рамках  традиционных  математических  формул.    Формальному  подходу  присуща  строгая  однозначность  интерпретации,  а  все,  что  связано  с  применением  естественного  языка,  имеет  многозначную  интерпретацию.  Прилагательное  «fuzzy»,  которое переводится  на   русский  язык  как  «размытый»,  «ворсистый», «нечеткий»,  введено  в название  новой  теории,  чтобы  разграничить  ее  с  традиционной  четкой математикой  и  аристотелевой  логикой,  оперирующих  с  четкими  понятиями: «истина – ложь»,  «включено -  не   включено».   Основатель  современной  концепции  нечеткой  логики   профессор Л. Заде  (L. Zaden)  построил  новую  математическую  дисциплину, в  основе  которой  лежит  не  классическая  теория  множеств,  а  теория  нечетких множеств.  Последовательно проводя  идею  нечеткости,  можно  описать   нечеткие  аналоги  всех  основных  математических  понятий  и  создать  аппарат нечеткой  логики  (НЛ) для  моделирования  человеческих  рассуждений  и  способов  решения  задач.  

Нечеткое  множество  -  это  формализация  лингвистической  информации  для  построения  математических  моделей.  В  основе  этого  понятия  лежит   представление  о  том,  что  составляющие  данное  множество  элементы,  обладающие  общим  свойством,  могут  обладать  им  в различной  степени, и,  следовательно,  принадлежать  к  этому  множеству  с  различной степенью.          

Сущность  НЛ  сводится к следующим  моментам:

-  в ней используются лингвистические переменные (вместо обычных числовых)  или  в  дополнение  к  ним;

-  простые отношения между переменными описываются с помощью нечетких высказываний;

-  сложные отношения определяются нечеткими алгоритмами.

Практическое  использование  НЛ  предполагает  наличие функций  принадлежности  (ФП),  которыми  описываются  лингвистические  переменные   «малый»,  «средний»,  горячий»  и т.д.  Под  ФП  будем  понимать  кривую,  указывающую, каким образом каждая точка входного пространства отображается  в  степень принадлежности между  0  и  1.    Для нахождения ФП могут быть использованы   различные    методы, например:  прямые;  косвенные;  посредством  типовых  форм;  по  данным  эксперимента.           Рекомендуется  использовать   типовые  формы  ФП,  в   частности,  треугольные,   трапециевидные, гауссовы и  другие.  Форма ФП определяется разработчиком системы, исходя из условий простоты, удобства и эффективности использования.  Например,   в   модуле   FuzzyLogicсистемы  Matlab,  применяемого   для решения  задач  посредством  НЛ,   имеется   одиннадцать  стандартных   видов  ФП. 

  1.2 Система  нечеткого  логического  вывода

Нечеткий  логический  вывод  -  это  аппроксимация  зависимости  «входы  -  выход»  на основе  лингвистических  высказываний  «если  -  то»  и  логических  операций  над  нечеткими множествами.  Типовая  структура  системы  нечеткого  вывода показана  на  рис.1. 

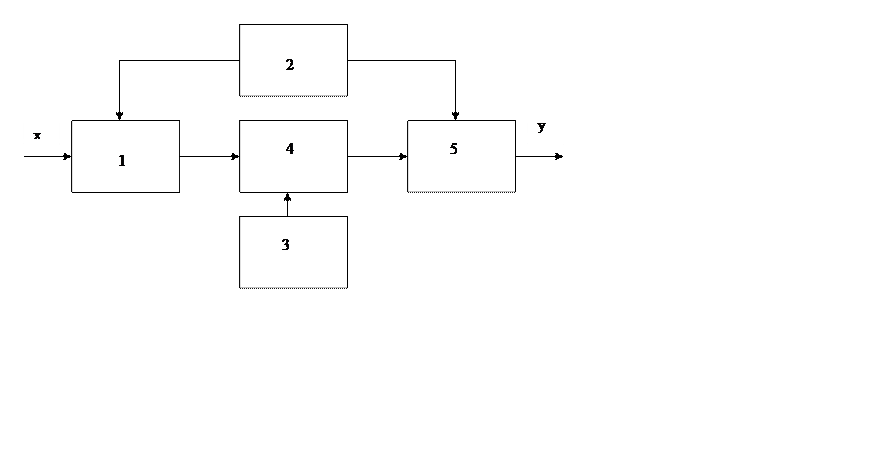
Рисунок  1  -  Система  нечеткого  логического  вывода 

(1 – фаззификатор;  2  -функции  принадлежности;  3  - нечеткая база  знаний;  4  -  машина нечеткого логического вывода;  5  -  дефаззификатор)

Система    логического  вывода  содержит следующие  модули:

·  фаззификатор  -  преобразует  фиксированный  вектор  влияющих  факторов  Х  в  вектор  нечетких  множеств  ,  необходимых   для  нечеткого  вывода;

·  функции  принадлежности  -  используются  для  представления  лингвистических  термов  в  виде  нечетких  множеств;

·  нечеткая  база  знаний  -  содержит информацию  о   зависимости  Y = f (X)  в  виде  лингвистических  правил:  если  -  то;

·  машина  нечеткого  логического  вывода  -  на  основе  базы знаний  определяет  значение  выходной  переменной  в виде  нечеткого  множества  ,  соответствующего  нечетким  значениям  входных  переменных   ;