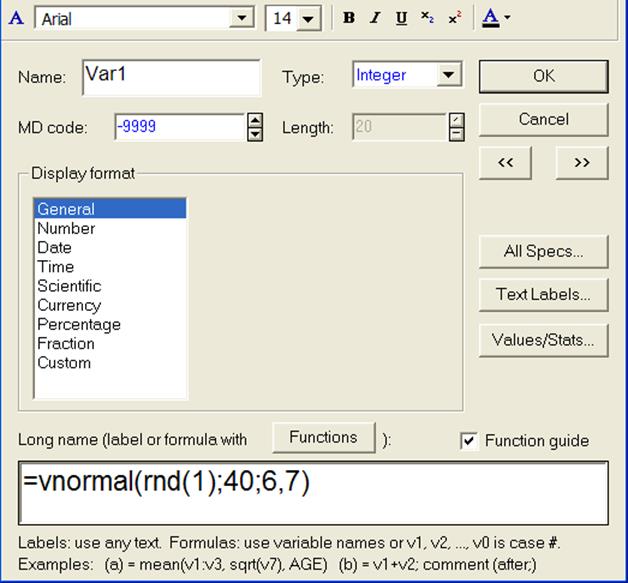
Рисунок 3 - Окно моделирования возраста клиента
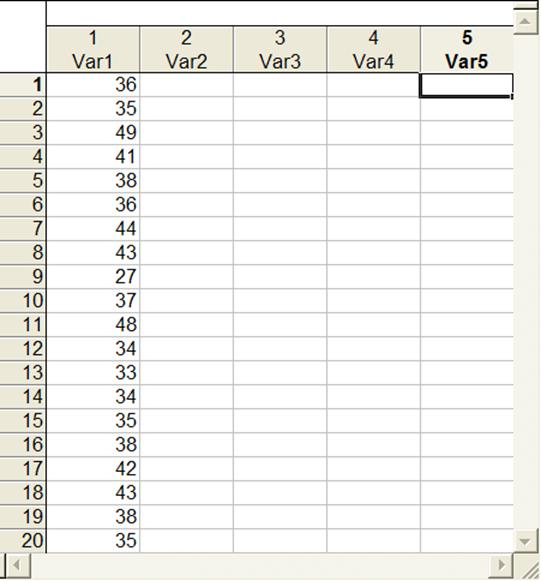
Рисунок 4 - Смоделированные значения возраста клиента
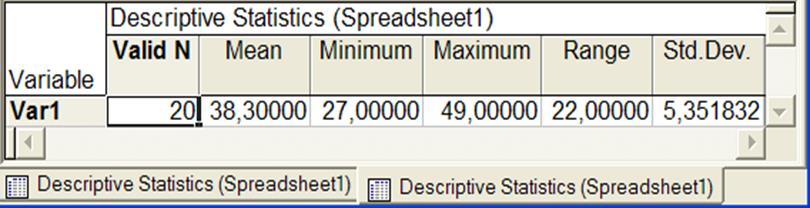
Рисунок 5 - Описательные статистики переменной Var1
Повторить эту процедуру для всех параметров рассматриваемого варианта. В итоге должна получиться полностью заполненная таблица, один из столбцов которой показан на рис.4.
4.3 Определение величины риска
Смоделированные значения входных переменных поочередно подставляются в окно ввода (рис.6), а над правым столбцом появляется значение выходной переменной (риска)
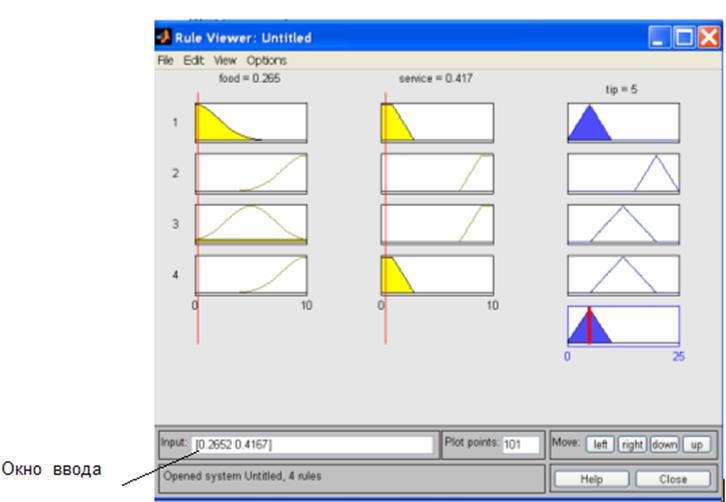
Рисунок 6 - Редактор правил с окном ввода входных переменных
Повторение этой процедуры для каждой строки входных данных приведет к тому, что в таблице, приведенной на рис.4, появится еще один столбец, где будут указаны величины риска, соответствующие определенной строке. Полученная таблица является основой для построения уравнения регрессии.
4.4 Определение уравнения регрессии
По последней таблице уравнение регрессии строится в пакете Statistica.6.0. Методика такого приема приведена подробно в методических указаниях по выполнению лабораторных работ по курсу прогнозирования, а здесь укажем лишь основные этапы.
Воспользуемся для иллюстрации файлом данных Poverty. Sta, который открывается через File - Open (Файл – Открыть).
1. Из меню Statistics - AdvancedLinear/NonlinearModels (Статистики-Расширенные линейные-нелинейные модели) выбрать GeneralLinearModels (Общие линейные модели) для отображения стартовой панели.
Выбрать в качестве типа анализа Multiple regression (Множественная регрессия) и в качестве метода решения - Quickspecsdialog (Быстрый диалог). Затем нажать ОК для входа в диалоговое окно множественной регрессии (рис.7).
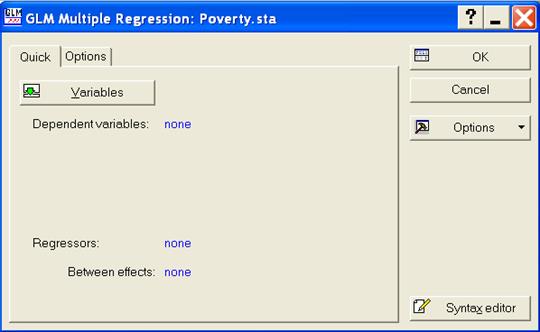
Рисунок 7 - Диалоговое окно множественной регрессии
При нажатии клавиши Variables в этом окне появляется окно выбора переменных (рис.8), в котором в качестве зависимой переменной следует указать признак Pt_Poor, а в качестве независимых - все остальные.
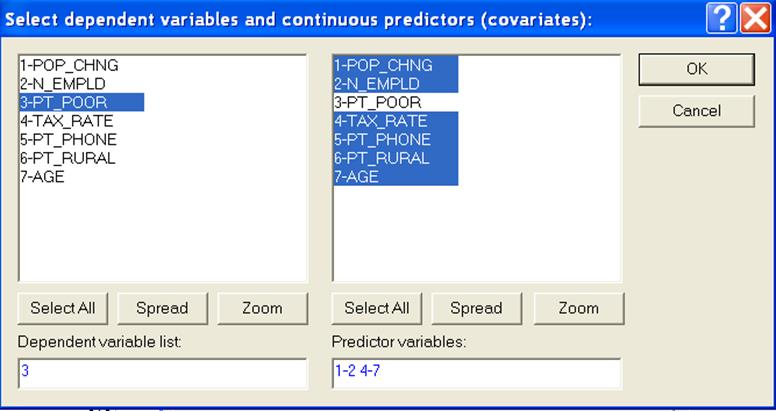
Рисунок 8 - Окно выбора переменных для множественной регрессии
(Отметим, что при определении переменных правого столбца вначале нужно выделить все переменные, а затем при нажатой клавише Ctrl отметить признак Pt_Poor). Далее - нажать ОК для возврата к диалоговому окну регрессии.
В задаче с реальными данными зависимой величиной является риск (выделить в левой части окна), а все остальные переменные - независимыми (отметить в правой части окна).
2. Нажав ОК в последнем окне, приходим к окну результатов регрессионного анализа, где при выделенной опции Summary (Итог) нужно нажать клавишу Coefficientsдля отображения рассчитанных коэффициентов регрессии между выделенными переменными. Полученные результаты приведены в табл.1.
Таблица 3 - Регрессионные коэффициенты

Эта таблица показывает регрессионные коэффициенты (В) и стандартизованные регрессионные коэффициенты (Beta). С помощью коэффициентов В устанавливается вид уравнения регрессии, которое в данном случае имеет вид
![]()
Включение в правую часть только этих переменных обусловлено тем, что лишь эти признаки имеют значение вероятности р меньше, чем 0,05 (см. четвертый столбец табл.3). Такое значение вероятности принято при вычислении доверительных интервалов на коэффициенты регрессии.
В рассматриваемой реальной задаче в левой части уравнения находится риск, а в правой - значимые для риска переменные. Анализ уравнения выявляет факторы, в наибольшей степени влияющие на риск, что позволяет наиболее эффективно управлять риском.
Лабораторная работа 4
Вычисление Value-at-Risk
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.