Представление исходных данных. Визуализация многомерных данных в среде Statistica (Лабораторная работа № 1), страница 10

Общее назначение множественной регрессии состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами) и зависимой переменной. Например, агент по продаже недвижимости мог бы вносить в каждый элемент реестра размер дома, число комнат, удаленность от  города и субъективную оценку привлекательности дома. Как только эта информация собрана для различных домов, было бы интересно посмотреть, связаны ли и каким образом эти характеристики дома с ценой, по которой он был продан. Например, могло бы оказаться, что число комнат является лучшим предсказывающим фактором для цены продажи дома в некотором специфическом районе, чем привлекательность дома (субъективная оценка). Могли бы также обнаружиться и «выбросы», т.е. дома, которые могли бы быть проданы дороже,  учитывая их характеристики.  
           Специалисты по кадрам обычно используют процедуры множественной регрессии для определения вознаграждения, адекватного выполненной работе. Можно определить некоторое количество факторов или параметров, таких, как «размер ответственности» или «число подчиненных», которые, как ожидается, оказывают влияние на стоимость работы. Кадровый аналитик затем проводит исследование размеров окладов среди сравнимых компаний на рынке, записывая размер жалования и соответствующие характеристики (т.е. значения параметров) по различным позициям. Эта информация может быть использована при анализе с помощью множественной регрессии для построения  уравнения.

В  вариантах  заданий  интерес  представляет  построение  уравнения,  связывающего  риск  с набором  входных  переменных.   При  этом может  оказаться,  что  часть  входных  признаков  не  оказывает  существенного  влияния   на  риск,  и этот  результат  имеет   для  менеджера  важное значение,  т.к.  в  дальнейшем  он  может  обращать  внимание  лишь на  значимые  входные  переменные.     

4 Работа  на  компьютере

4.1 Построение  системы  нечеткой логики

Проводится  в  модуле  Fuzzy  Logic  системы  Matlab  аналогично тому,  как  это  выполнялось  в лабораторной  работе  2.

4.2  Моделирование  входных переменных

Для  моделирования, проводимого  в пакете   Statistica.6.0, необходимо  знать  вид  распределения,  которым описывается   данная  переменная,  среднее значение  (СЗ)  и  среднеквадратичное  отклонение  (СКО).  Без  потери  общности  примем,  что  каждый  из параметров  распределен  по  нормальному  закону.  СЗ  определяется  из  диапазона,  который  установлен  для каждой  переменной   в п.1.  Например,  возраст  клиента,  обратившегося за  кредитом,  изменяется  от 20  до  60  лет.  В этой  ситуации  СЗ  составляет  40  лет.  Для  нахождения  СКО  учтем, что весь  диапазон  изменения возраста  при  нормальном распределении  практически  укладывается  в  диапазон  3 СКО  от  среднего,  откуда  СКО  составляет  величину,  равную 6,7 года.

Далее  процедура  моделирования  состоит  из  следующих  шагов:     

·  Открыть  новый  файл,  состоящий  из 20 строк  и 5   столбцов  (рис.2).  Число  столбцов  определяется количеством  переменных в  данном варианте.

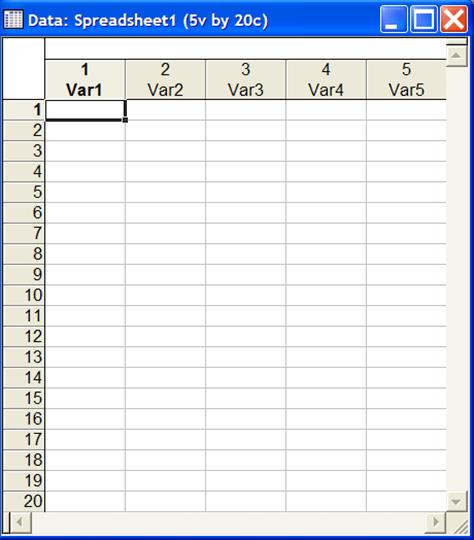
Рисунок  2  -   Новый файл в  пакете  Statistica

·  Через  меню  Data – VariableSpecs… вызвать  окно  определения  переменной,  в  нижней  части  окна  написать  формулу  =vnormal(rnd(1);40;6,7)  (рис.3) и после   нажатия  ОК  в  первом столбце  появятся  20 чисел,  представляющих  смоделированные  значения  первого  признака  (рис.4).  Данная  процедура  является  моделированием  методом  Монте-Карло  значений  нормально распределенных  величин  по  СЗ  и СКО.  Обратить  внимание на  то,  что при каждом  розыгрыше  в формулу подставляются  значения СЗ и СКО  для   данной  переменной.  Кроме того,  для  типа  переменной  необходимо   выбрать опцию  Integer (целые).  Можно убедиться, что  разыгранные  величины  имеют  описательные статистики, близкие  к  найденным  СЗ  и  СКО  (рис.5).   Для  построения  таблицы  на рис.5  необходимо:  нажать Statisticsв верхней  строке,  затем BasicStatistics/TableиDescriptiveStatistics,  после  чего  в  окне выбрать  необходимые  параметры.