Лабораторная работа 1
Представление исходных данных
Цель работы: ознакомить студентов с видами представления исходных данных и обучить практическим навыкам визуализации многомерных данных в среде Statistica.
1 Теоретические сведения
1.1 Виды представления многомерных данных
Независимо от природы
наблюдаемых явлений или процессов в большинстве ситуаций исходные данные
представляются в виде матрицы (таблицы) объект-признак, где строками
являются объекты, а столбцами ─ признаки. Под объектом подразумевается любой
предмет изучения, например, страна, фирма, регион, студенческая группа и т. п.
Признак определяет характеристики рассматриваемого объекта, например, если
объектом исследования является фирма, то к числу признаков, ее характеризующих,
можно отнести численность персонала, ежемесячный объем расходов и доходов,
число контрагентов и другие характеристики. Каждый элемент такой матрицы Х
обозначается как xij, где ![]() - номер объекта;
- номер объекта; ![]() - номер признака. Размерность этой матрицы составляет
- номер признака. Размерность этой матрицы составляет ![]() . Матрица Х описывает m объектов в терминах n признаков, причем значения m и nобычно достаточно велики. Считается, что для
получения статистически достоверных результатов число объектов должно
превышать число признаков в несколько раз.
. Матрица Х описывает m объектов в терминах n признаков, причем значения m и nобычно достаточно велики. Считается, что для
получения статистически достоверных результатов число объектов должно
превышать число признаков в несколько раз.
При обработке многомерных данных следует учитывать дуализм представления, так как имеются возможности визуализации как объектов в пространстве признаков, так и признаков в пространстве объектов. Кроме представления исходных данных в виде матрицы объект-признак, имеются и другие возможности представления. Например, с помощью коэффициента корреляции между признаками, который вычисляется по формуле
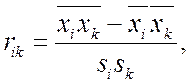
где 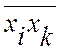 ─ среднее значение произведения величин признаков xi, xk;
─ среднее значение произведения величин признаков xi, xk; ![]() ,
, ![]() ─ среднее значение признака xi, (xk); si (sk) ─ среднеквадратичное отклонение соответствующих
признаков, можно представить исходные данные в виде матрицы признак-признак.
─ среднее значение признака xi, (xk); si (sk) ─ среднеквадратичное отклонение соответствующих
признаков, можно представить исходные данные в виде матрицы признак-признак.
Эта матрица R в отличие от предыдущей имеет
размерность ![]() . В каждой ячейке матрицы расположены
значения коэффициента корреляции между соответствующими признаками; на
диагонали матрицы стоят единицы, так как корреляция признака с самим собой
максимальна и равна единице. Матрица симметрична относительно своей диагонали.
. В каждой ячейке матрицы расположены
значения коэффициента корреляции между соответствующими признаками; на
диагонали матрицы стоят единицы, так как корреляция признака с самим собой
максимальна и равна единице. Матрица симметрична относительно своей диагонали.
Сходство или различие между классифицируемыми объектами устанавливается в зависимости от метрического расстояния между ними. Если каждый объект описывается n признаками, то он может быть представлен как точка в n -мерном пространстве, и его сходство с другими объектами будет определяться как соответствующее расстояние. Указанное обстоятельство позволяет перейти к еще одному виду представления исходных данных, а именно, к матрице D объект-объект, представляющей собой таблицу расстояний между анализируемыми объектами. В этом случае в каждой ячейке матрицы находится величина расстояния, допустим, евклидова, рассчитываемого по формуле:
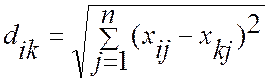 .
.
Здесь xij, xkj ─ значения j-го признака, соответственно, у i-го и k-го объектов.
На диагонали матрицы находятся нули, поскольку расстояние от точки до нее самой равно нулю. Элементы матрицы симметричны относительно диагонали.
Таким образом, исходные данные могут быть представлены в виде матриц трех типов:
· матрицы объект-признак;
· матрицы признак-признак;
· матрицы объект-объект.
Визуализация многомерных данных
Любое исследование многомерных данных невозможно без использования метода главных компонентов (ГК). Сущность этого метода заключается в снижении размерности данных путем определения незначительного числа линейных комбинаций исходных признаков, которые объясняют большую часть изменчивости данных в целом. Метод ГК связан с переходом к новой системе координат, которая является системой ортонормированных линейных комбинаций. Этот метод дает возможность по n исходным признакам объектов построить такое же количество ГК, являющихся обобщенными (агрегированными) признаками. На первый взгляд, такой переход не дает никакого преимущества в представлении данных, но существует возможность сохранения информации о рассматриваемых данных даже в том случае, если сократить количество вычисленных ГК. Кроме того, при сохранении двух или трех ГК реализуется возможность визуализации многомерных объектов в сокращенном признаковом пространстве. Метод ГК обладает рядом свойств, делающим его эффективным для визуализации структуры многомерных данных. Все они касаются наименьшего искажения геометрической структуры точек (объектов) при их проектировании в пространстве меньшей размерности.
Математическая модель ГК базируется на допущении, что значения множества взаимосвязанных признаков порождают некоторый общий результат. В этой связи при представлении исходных данных как раз и важна матрица признак-признак, в которой содержится вся информация о попарной связи между признаками.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.