
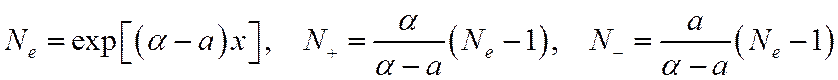
Здесь α – коэффициент ионизации, a – коэффициент прилипания. Все нарождающиеся электроны летят
к аноду одной rруппой со скоростью дрейфа Vd=μeE0. Однако вследствие диффузии электронное
облако расплывается около центральной точки x0=Vдt.
Плотность электронов в облаке ne(x, r, t) подчиняется общему ypaвнению
диффузииНернста-Планка,
в котором должны быть приняты во внимание дрейфовое движение, рождение и гибель
электронов.
 (17)
(17)
q+ - число родившихся (вследствие ионизации) электронов на единицу объема в единицу времени, q- - число погибших (вследствие рекомбинации и прилипания) электронов на единицу объема в единицу времени.
Рассмотрим начальный этап развития лавины, когда концентрация электронов невелика и рекомбинацией можно пренебречь. В этом случае, как отмечено выше, можно использовать коэффициенты ионизации и прилипания, и уравнение (17) удастся решить аналитически. Через коэффициенты ионизации и прилипания выражаем число родившихся и погибших электронов в единице объема:
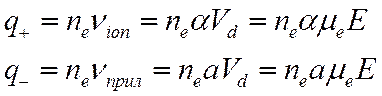
Уравнение (17) преобразуется к виду:
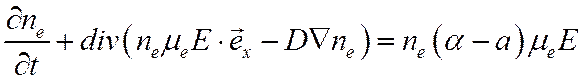
Задача имеет цилиндрическую симметрию, от угловой координаты величины не зависят. Операторы дивергенции и градиента имеют в этом случае вид:
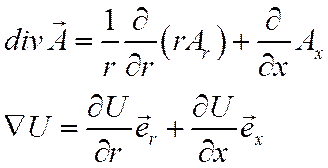
Учитывая эти формулы, можно переписать дивергенцию первого слагаемого:
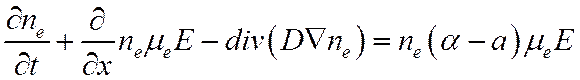 (18)
(18)
Сделаем замену переменной – введем вместо старой продольной координаты x новую координату ξ, по следующей формуле:
![]()
Новые координаты – ξ, r, t (время входит как равноправная координата!). Вспомним формулы перехода от старого набора координат a1,a2,…,an к новому b1,b2,…,bn. Частные производные в старых координатах заменяются на частные производные в новых координатах по правилу:
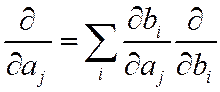
В нашем случае частная производная по радиальной координате остается без изменений, частная производная по x:
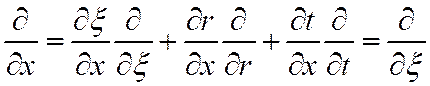
Частная производная по t меняет вид:
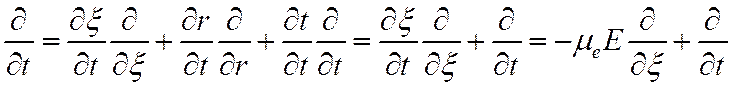
Запишем теперь (18) в новых координатах:
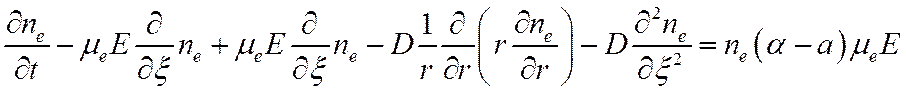
Второе и третье слагаемые сократились, и мы получаем:
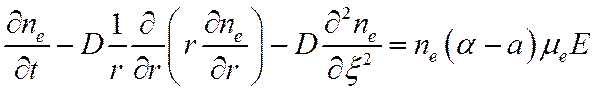 (19)
(19)
Теперь сделаем еще одну замену. Вместо концентрации электронов ne(ξ,r,t) введем новую неизвестную ñe:
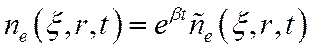 (20)
(20)
Подставляя (20) в (19), мы получаем:
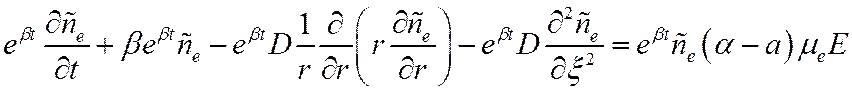
Видно, что если взять β=(α-a)μeE, второе и последнее слагаемое сокращаются. И мы получаем уравнение:
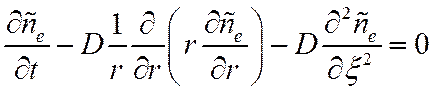 (21)
(21)
Это уже обычное уравнение диффузии, оно имеет решение:

Возвращаясь к исходным переменным, мы получаем решение исходного уравнения (18):
Решение уравнения имеет вид:
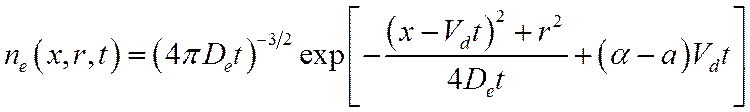 (22
(2213)
Плотность ne падает с расстоянием от движущегося центра по гауссову закону. Радиус сферы, на которой плотность ровно в e раз меньше, чем плотность в центре nе(х0,0,t), растет с течением времени (или по мере продвижения лавины) по характерному для диффузии закону:
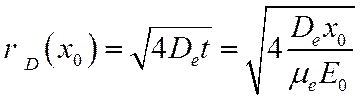
За время пролета лавины до анода ионы практически не успевают сдвинуться с места. Поэтому в каждом месте они накапливаются. Плотность положительных ионов составляет:
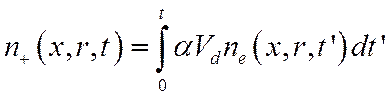
Чтобы получить n-, нужно α заменить на а.
Функция ne в
интеграле задается формулой (2213).
В отсутствие прилипания в пределе t→∞ и не слишком далеко от оси приближенное
вычисление интеграла дает:
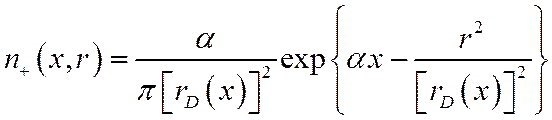
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.