Лавинный механизм в сильном электрическом поле, страница 7

Ионизация, из-за высокого порога, обычно является второстепенным каналом затрат энергии, в некоторых газах большая часть энергии уходит на возбуждение и значительная часть – на диссоциацию.

Сечения реакций и пробеги.

Для расчета разрядного процесса необходимо знать частоты столкновений каждого типа – упругих и неупругих. Из этих величин можно получить подвижность электронов, число электронов, родившихся в результате ионизации, интенсивность излучения.

Процесс столкновения электрона с молекулой описывается в рамках квантовой механики и, в принципе, возможен расчет частоты процесса. Однако такие расчеты очень трудоемки и до сих пор дают, зачастую, лишь удовлетворительное соответствие с экспериментом. Поэтому расчет опирается на экспериментальные данные по конкретным реакциям.

В принципе, можно получить экспериментально длину пробега по данной реакции l. Длина пробега – среднее расстояние, которое проходит электрон между столкновениями данного типа. Однако длина пробега неудобна прежде всего потому, что зависит от концентрации нейтральных молекул, l ~ n^-1. То есть к экспериментальным данным необходимо было бы добавлять информацию о том, при каком давлении проводился эксперимент и каков был состав газа.

Более удобной величиной для характеристики вероятности реакции является сечение σ. Эту величину можно ввести как коэффициент: по определению частота столкновений электрона ν с нейтральной молекулой равна:

                                                                                              (1511)

V – скорость электрона (истинная скорость при столкновении с молекулой – то есть тепловая при низких напряженностях поля, направленная при высоких напряженностях.

σ –сечение реакции.

n₀ – концентрация нейтральных молекул.

Как видно из формулы (1511), сечение σ имеет размерность площади – м². С этим связана наглядная аналогия. Представим, что молекулы – твердые шарики радиуса r, а электрон – материальная точка. Столкновение происходит, когда электрон коснется поверхности шарика. Тогда частота столкновений будет даваться именно формулой (1511) с сечением рассчитанным по формуле σ=πr².

Сечение связано с длиной пробега следующим образом:

                                                                    

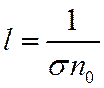
Сечения вводятся для столкновения каждого типа – сечение ионизации, сечение диссоциации, сечение возбуждения электронного уровня. Продолжая аналогию, молекулу с точки зрения электрона можно представить как мишень, на которой кольца разной площади соответсвуют разным типам столкновения. Площадь колец равна сечению данной реакции. Чем больше сечение реакции, тем больше ее вероятность.

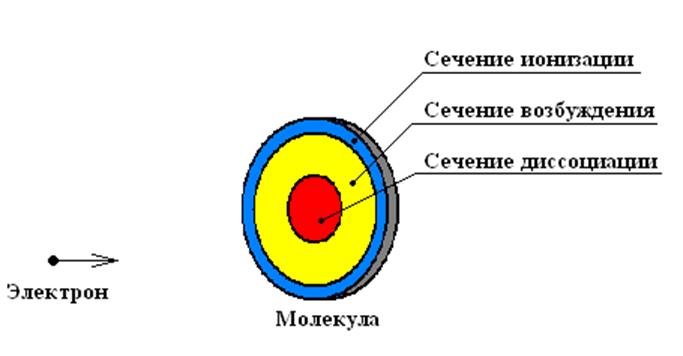
Рисунок 109. Наглядное представление о сечении разных реакций – молекула в виде мишени, кольца разной площади соответствуют разным типам столкновений. Площадь кольца равна сечению данной реакции.

Вероятность столкновения значительно зависит от энергии электрона, поэтому сечение является функцией энергии электрона σ(ε). Примеры экспериментальных кривых приведены на рисунке 1110. Вид функции σ(ε) обычно достаточно сложный, но есть общие закономерности.

Упругое столкновение не имеет энергетического порога, и величина сечения, как правило, не сильно меняется в интересующем нас диапазоне примерно до 30 эВ (рисунок 1110). Сечения неупругих столкновений имеют пороги – ниже пороговой энергии они равны нулю. Сечение упругих столкновений примерно на порядок больше сечений неупругих столкновений.

 

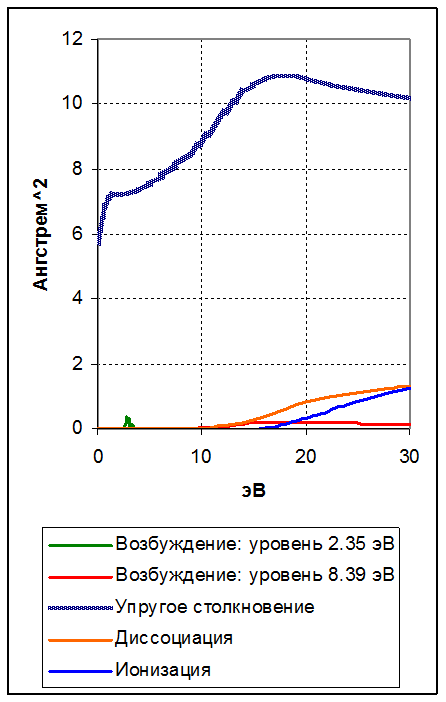
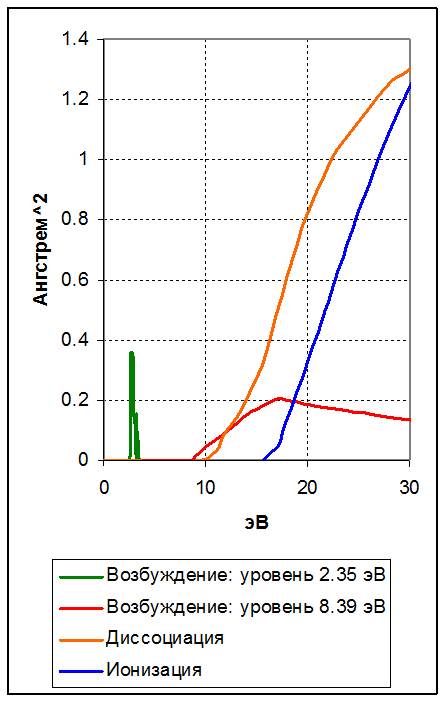
Рисунок 1110. Сечения разных столкновений электрона с молекулой азота N2. Экспериментальные данные.

Отрицательные ионы.

Некоторые атомы, например, кислород O, хлор Cl, фтор F, обладают отрицательным сродством к электрону. Это значит, что состояние атома с присоединенным электроном для них более энергетически выгодно, чем состояние нейтрального атома. Разность энергий между этими состояниями называется энергией сродства к электрону или просто сродством к электрону. Так, для атома кислорода O эта величина составляет 1,47 эВ.