Если электрон сталкивается с атомом кислорода O, молекулой кислорода O2, молекулой воды H2O, с высокой вероятностью происходит прилипание – образуется отрицательный ион O-, O2- или OH-.
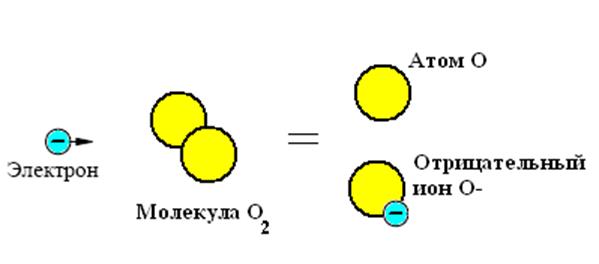
Рисунок 1211.
Один из механизмов прилипания.
Из-за прилипания в воздухе нет свободных электронов, поскольку в среднем за 11 наносекунд (1,1∙10-8 с) образовавшийся из-за воздействия космического излучения электрон прилипает к молекуле кислорода или воды.
Необходимые для расчета разряда свойства реакции описываются сечением, точнее, зависимостью сечения реакции от энергии электрона σ(ε). Однако для оценок и инженерных расчетов существует более удобная величина – число столкновений на единицу длины по дрейфу. Для ионизации эта величина называется просто коэффициент ионизации α, для прилипания – коэффициент прилипания a. В качестве аргумента функции берут не энергию электрона, а напряженность поля E, поскольку исходно в задаче известна именно она.
В результате, мы можем представлять, что электрон движется по силовой линии электрического поля и испытывает на единице длины α(E) ионизаций и a(E) прилипаний.
В отличие от сечения, α и a зависят от давления. Для α справедлив закон подобия:
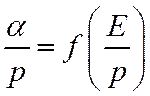
Здесь f – некоторая функция, специфичная для данного газа.
Лавинный процесс возможен, если вероятность прилипания меньше, чем вероятность ионизации, тогда число электронов в лавине будет нарастать. Это будет выполняться при:
![]() (16
(1612)
α>a. При E→0
коэффициент ионизации α стремится у нулю, а коэффициент прилипания, напротив,
стремится к бесконечности. Дело в том, что у ионизации есть энергетический порог,
и в отсутствии источника энергии электрону его не преодолеть, у реакции
прилипания порога нет, она энергетически выгодна. Таким образом, условие (1612)
устанавливает нижнюю границу напряженности, при которой возможно развитие
лавины. При меньшей напряженности лавина быстро затухает. При
атмосферном давлении в воздухе эта граница составляет около 24,5 кВ/см.
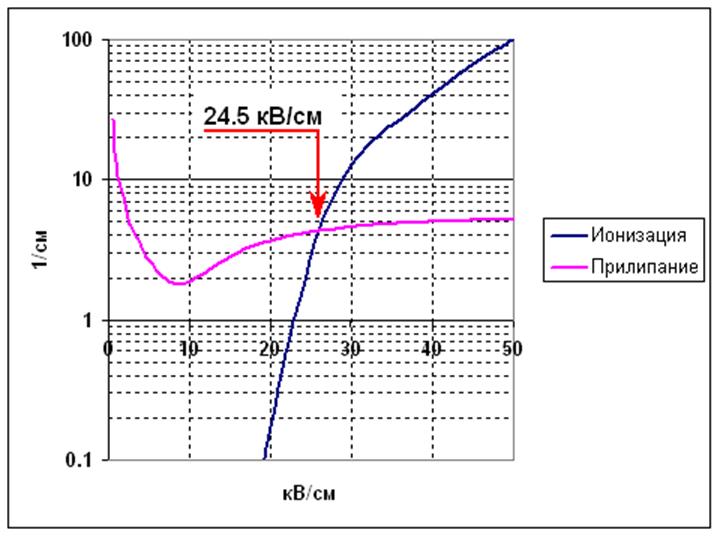
Рисунок 1312.
Коэффициенты ионизации и прилипания в зависимости от напряженности
электрического поля. Атмосферное давление.
Важно помнить, что границы применимости коэффициентов прилипания и ионизации уже, чем границы применимости сечения реакции. Основное условие – электрон сталкивается только с нейтральными невозбужденными молекулами, столкновениями с «вторичными частицами» можно пренебречь. Под вторичными частицами понимаются все те частицы, которых нет в исходном составе газа – они появляются в результате разрядного процесса. Это ионы, возбужденные молекулы, продукты диссоциации. В том числе необходимо пренебрегать и столкновениями электронов между собой. Таким образом, коэффициенты ионизации и прилипания применимы при малых концентрациях электронов.
Простейший механизм разряда – лавина. Она начинается с одного электрона (т.н. затравочный электрон). Разгоняемый электрическим полем, электрон дрейфует вдоль силовой линии. Если поле достаточно высоко, через некоторое время происходит ионизация, электронов становится два. Каждый из них через некоторое время вновь ионизует, таким образом, число электронов быстро («лавинообразно») возрастает.
При этом электроны движутся хаотично, а не строго вдоль силовой линии, поэтому контуры лавины – размытые, она напоминает облако электронов, растущее и дрейфующее вдоль силовой линии.
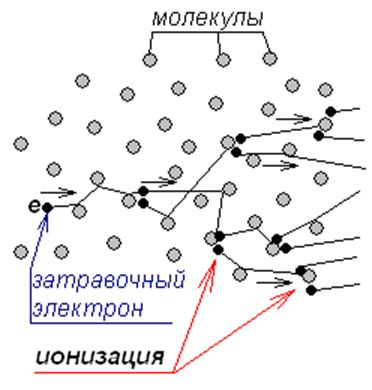
Рисунок 1413.
Одиночная электронная лавина.
Рассмотрим лавину в однородном внешнем поле Е между плоскими электродами. Пусть она начинается от одного электрона, вылетевшего с катода в момент t=0. Ось х направим от этого места катода в сторону анода.
Введем цилиндрические координаты, Ррадиальное
расстояние от оси х обозначаем r. С
учетом возможного образования отрицательных ионов полные числа электронов и
ионов нарастают по мере продвижения лавины как:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.