Лавинный механизм в сильном электрическом поле, страница 15

Здесь N – число электронов в лавине. Поскольку скорость ионов много меньше скорости электронов, в формуле (3141) эффективно работает только второе слагаемое. Таким образом, ток возрастает экспоненциально – как число электронов:

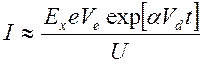                                                                                (3242)

По формуле (3242) и находят коэффициент α на опыте, измеряя зависимость I(t). Нужно отметить, что применение такого метода требует знания дрейфовой скорости электронов. Значение дрейфовой скорости электронов в линейной фазе лавины можно считать однородным в пространстве и не меняющимся во времени, поскольку спектр электронов, а значит и подвижность, определяется напряженностью поля.

 

Сложность применения данного метода в CFD-ACE состоит в том, что явно ток на электродах в файл результатов не выводится. Единственный Один из путьей его расчета – подсчет заряда на электродах. Для этого можно воспользоваться законом Гаусса:

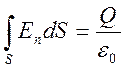                                                                                             (3343)

Проинтегрировав нормальную компоненту поля по поверхности электрода, мы получим заряд Q. Далее необходимо анализировать зависимость Q(t). Дополнительная сложность состоит в том, что в линейной фазе лавины (для которой и вычисляется коэффициент α) возмущение на фоне однородного поля очень мало.

Что касается соответствия метода анализа тока I и метода, связанного с прямым подсчетом числа электронов в лавине, соответствие между ними становится ясно из формулы (3141), которая, отмечу, является точным результатом. Ведь само использование метода измерения тока основано на утверждении, что ток пропорционален числу электронов в лавине.

Расчет тока по численному решению проведен для случая поля E=80 кВ/см. Чтобы на фоне однородного поля было заметно собственное поле объемного заряда, пришлось взять достаточно большую начальную концентрацию электронов: 10¹⁶ 1/м³. Подсчитывался заряд на катоде, поскольку он ближе к лавине, и поляризационный заряд достаточно быстро спадает при удалении от оси симметрии. Это важно, поскольку модель конечна.

Из решения CFD-ACE была получена в виде таблицы зависимость нормальной компоненты электрического поля En на электроде от радиальной координаты r. Это позволило численно подсчитать поляризационный заряд Qп по формуле:

                                                            

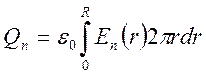
Здесь R – радиус модели CFD-ACE. Зависимость Qп(t), как оказалоськак и должно быть по формуле (32), хорошо аппроксимируется формулой:

                                                                              (3444)

По формуле (3444) находим аппроксимацию для тока:

                                                                                    (3545)

На рисунке 3032 показаны результаты расчета: поляризационный заряд на катоде и ток в цепи. При малых временах заряд положителен, поскольку в начале задается компактная область, заполненная электронами, а положительных ионов в начальный момент нет. Для экранирования отрицательного объемного заряда необходим положительный поверхностный заряд. Затем, при удалении лавины, положительный заряд перетекает на анод. Ток на катоде взят по модулю.

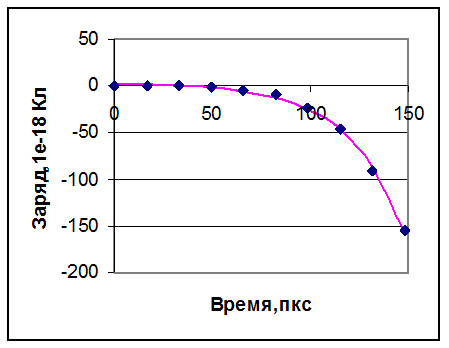
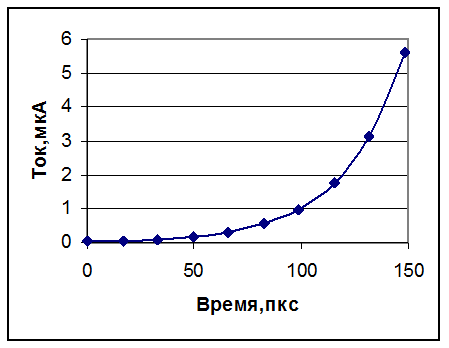
Рисунок 3032. Поляризационный заряд на катоде (слева). Сплошной линией показана аппроксимация по формуле (3444). Ток на катоде (справа).

Сравнение зависимости (3545) с теоретически обоснованной формулой (3242) позволяет вычислить коэффициент α так, как это делается в реальном опыте. Именно:

                                                                 

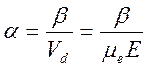
Коэффициент β, найденный аппроксимацией по формуле (3545), оказался равен 4,39∙10¹⁰ 1/с, с погрешностью аппроксимации 5%. Подвижность электронов, выводимая CFD-ACE в файл решения, практически одинакова по всей лавине и равна 0,036 м²/(В∙с). Учитывая, что напряженность внешнего однородного поля равна 80 кВ/см, получаем α=0,152 1/мкм. Эмпирическая формула (2424)  дает значение 0,16 1/мкм, то есть наблюдается хорошее соответствие.