Лавинный механизм в сильном электрическом поле, страница 4

Рассмотрим движение электрона в однородном электрическом поле в газе из одинаковых нейтральных молекул. Между столкновениями электрон движется, взаимодействуя лишь с электрическим полем, так что справедлив второй закон Ньютона:

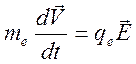                                                                                                (51)

Акт взаимодействия электрона с молекулой происходит очень быстро по сравнению со временем пробега между столкновениями. Оценки показывают, что время взаимодействия можно оценить в 10^-16 с, тогда как время между столкновениями составляет порядка 10^-12 с. Так что столкновения можно учесть как мгновенное изменение скорости ΔV_i в i-м столкновении. Тогда в уравнение (51) добавляется слагаемое, описывающее столкновения:

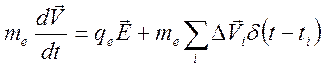                                                                (62)

Данное уравнение точно описывает дрейф с мгновенными столкновениями, однако не дает продвинуться в вычислениях.

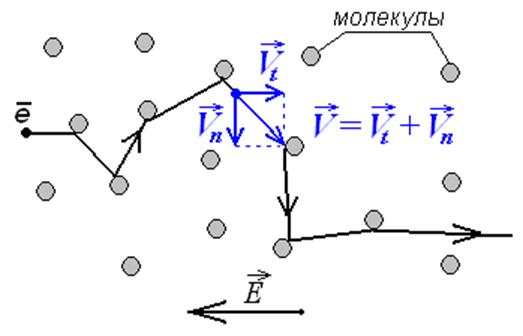
Рисунок 54. В любой точке скорость электрона V можно разложить на составляющую вдоль поля вдоль поля V_t и нормальную к полю составляющую V_n.

Как уже было сказано, масса электрона m_e мала по сравнению с массой молекулы M. Можно считать, что упругое столкновение поворачивает скорость электрона, но не меняет модуль скорости. Проведем усреднение уравнения (62) в таком приближении. Задача имеет одно выделенное направление – вдоль вектора электрического поля E. Перпендикулярные к нему направления равноправны, поэтому разложим вектор V на составляющую вдоль поля V_t и нормальную к полю составляющую V_n (рисунок 54). V = V_t + V_n. Усредняя уравнение (62), имеем выражение:

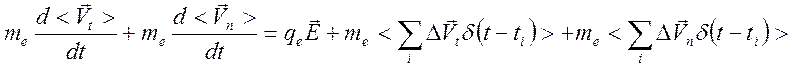                                                                           (73)

Усреднение изменений нормальной компоненты скорости дает ноль из-за осевой симметрии задачи. То же касается собственно скорости электрона. Усреднение ее нормальной к полю составляющей V_n дает ноль. Здесь нужно отметить, что ноль получается при усреднении вектора нормальной составляющей, но, например, усреднение <V_n²> даст ненулевую величину, ведь электрон отбрасывает ударами и поперек поля. Просто выделенного направления поперек поля в данной задаче появиться не может.

Это касается и продольной составляющей. При активном тепловом движении много электронов движется по полю, значительное число – против поля, и <V_t> образуется за счет разности этих потоков, но мы ничего не можем сказать о <V_t²>, она может быть значительно больше <V_t>². Отсюда важный вывод – зная <V_t> и <V_n> = 0, мы, тем не менее, не имеем никакой информации о кинетической энергии, которая есть:

                                                    

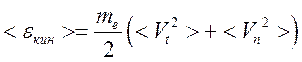
Поскольку нормальные компоненты векторов в уравнении (73) нулевые, остается уравнение, где присутствуют лишь продольные компоненты векторов:

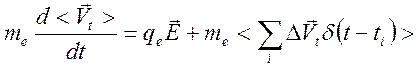                                                (84)

Переходя от уравнения (73) к уравнению (84), мы теряем возможность говорить о средней величине модуля скорости. Оно позволяет лишь следить за усредненным перемещением электрона в пространстве на масштабах много больше пробега между столкновениями.

Если электрон перед ударом двигался вдоль силовой линии поля, а при столкновении отклонился на угол θ, мы имеем картину столкновения, показанную на рисунке 65.

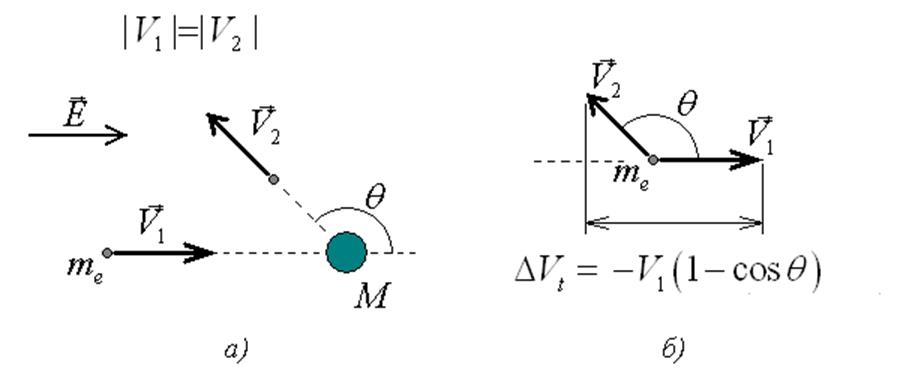
Рисунок 65. а) - модель упругого столкновения с не меняющейся по величине скоростью электрона. Скорость электрона до столкновения направлена вдоль вектора напряженности поля. б) – подсчет изменения продольной составляющей скорости.

Как продемонстрировано на рисунке 65, в этом случае легко считается изменение продольной составляющей скорости. Оно пропорционально величине скорости до столкновения и связано с углом отклонения θ.

                                                                                     (95)

В таком случае уравнение (84) переписывается в виде:

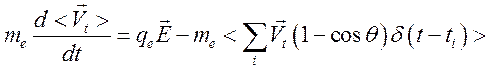                                                                                                               (106)