Лавинный механизм в сильном электрическом поле, страница 3

Изложенные выше представления будут работать при высоких значениях E/p. При атмосферном давлении можно считать, что направленное движение вдоль электрического поля преобладает над тепловым при полях свыше 100 кВ/см, но разрядные процессы возможны уже при напряженности 25 кВ/см. Здесь ионизация происходит уже за счет тепловой энергии, и необходимо более аккуратно описывать движение электрона в воздухе.

Электрон в воздухе в присутствии электрического поля.

Математическое описание дрейфаУпругое соударение легкой и тяжелой частиц.

Электрическое поле увлекает электрон. Однако движению вдоль силовой линии препятствуют упругие удары, в результате которых направление движения электрона меняется. Упругий удар - удар, при котором суммарная кинетическая энергия частиц до и после столкновения одинакова, она не переходит в другие виды энергии. Масса электрона во много раз меньше массы атомамолекулы, поэтому при упругом ударе он может обменяться с атомом молекулой малой долей своей энергии. Покажем это.

Рассмотрим упругое столкновение в системе отсчета, где тяжелая частица  (молекула) покоится. Масса легкой частицы m, ее начальная скорость v₁, конечная v₂. Направление начальной скорости v₁ совпадает с осью x. После столкновения направление движения легкой частицы изменяется на угол θ. Масса тяжелой частицы M, до удара она покоится, ее скорость после удара – V (рисунок 3).

 

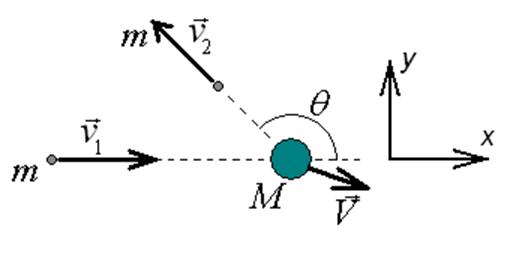
Рисунок 3. К расчету упругого столкновения.

 

Запишем законы сохранения импульса и энергии:

                                            

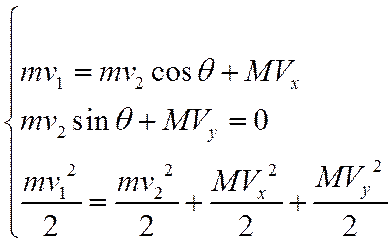
Зная v₁ и угол отклонения легкой частицы θ, мы можем найти три неизвестных – v₂, V_x и V_y. Выразив V_x и V_y через v₁, v₂ и θ в первом и втором уравнении, подставляем результаты в третье. Получаем:

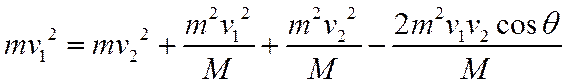                                                                                                          (1)

Это квадратное уравнение на v₂, величины v₁ и θ выступают здесь как параметры. Разрешая уравнение (1), получаем:

             

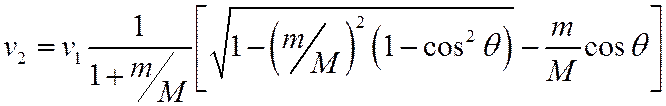
Это точное решение уравнения (1) для любых m и M, пока мы не делали никаких приближений.

Далее нас интересует случай m < M. Видно, что при m/M→0 v₂→v₁, при этом после столкновения скорость уменьшается, v₂ < v₁. Поэтому рассмотрим относительное изменение скорости легкой частицы:

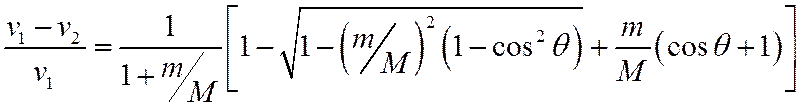
Оценим это выражение сверху для случая 0≤m/M≤1. Очевидно:

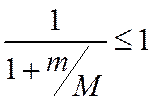                                                                                              (2)

Нетрудно показать, что для 0≤x≤1 выполняется:

                                                               

Отсюда получаем оценку:

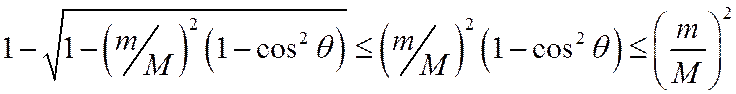                                                                              (3)

Учитывая оценки (2) и (3), получаем для относительного изменения скорости оценку:

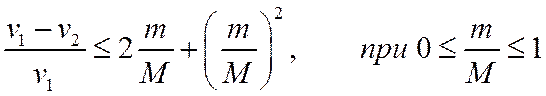                                                                                                             (4)

При малых отношения m/M квадратичным слагаемым в правой части можно пренебречь. Получим еще оценку для относительного изменения кинетической энергии легкой частицы:

               

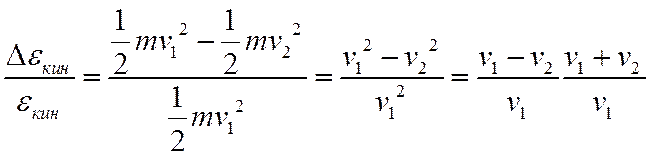
Используя то, что 0≤v₂≤v₁, а также оценку (4), получаем:

                               

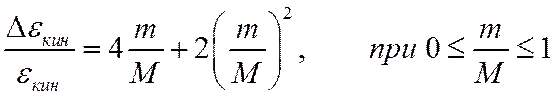
И вновь, при малых значениях параметра m/M квадратичным слагаемым можно пренебречь.

В нашем случае легкая частица – электрон, тяжелая – молекула.Именно, если энергия электрона ε_кин, справедлива оценка для изменения энергии в ходе столкновения Δε_кин:

                                                               

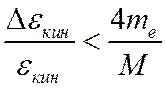
Здесь m_e – масса электрона, M – масса молекулы. Например, Ддля молекулы O₂ отношение 24m_e/M равно 36,48∙10^-5. Таким образом, молекулы для электрона – тяжелые, практически неподвижные шары. При столкновении электрон почти не теряет кинетической энергии, не передает ее молекуле.

Математическое описание дрейфа.

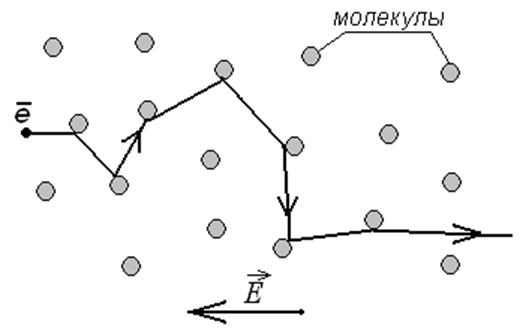
Рисунок 43. Движение электрона в однородном электрическом поле в газе из одинаковых нейтральных молекул.