Если предположить, что функция (2516)
с достаточной точностью описывает решение CFD-ACE, легко восстановить параметры зависимости. Задача
обладает симметрией – понятно, что центр облака лежит на оси симметрии X, поэтому для его определения достаточно
проинтегрировать концентрацию по оси X.
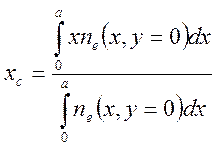
По зависимости координаты центра лавины от времени можно определить скорость дрейфа. Для этого следует аппроксимировать зависимость x(t) функцией:
![]()
Далее, зная координаты центра, можно определить ширину облака электронов в двух перпендикулярных направлениях:
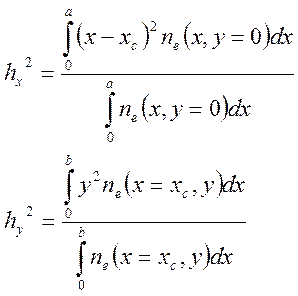 (27
(2718)
Запишем формулу (2516)
для некоторого момента времени в виде, удобном для расчета:
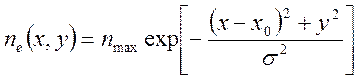 (28
(2819)
Здесь nmax – значение
концентрации в максимуме, а σ – параметр, имеющий смысл характерной
ширины облака и равный: ![]() .
.
Очевидно, что ширина облака hx или hy связана с параметром σ. Именно, если справедлива
формула (2819),
выполняется:
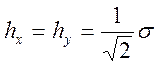
Таким образом, для определения параметра σ необходимо
взять только линейные интегралы (2718).
Если еще найти максимальную концентрацию nmax, можно
просто подставить известные параметры в формулу (2819)
и найти полное число электронов по формуле:
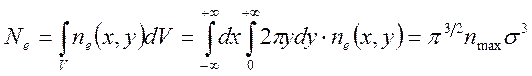 (29
(2920)
Таким образом, для нахождения полного числа электронов в
пространстве оказывается необходимым брать лишь одномерные интегралы. Однако
возникает проблема – в сильных полях форма электронного облака не описывается
функцией (2516).
Оно вытягивается вдоль поля. Можно пытаться обойти эту проблему, рассматривая
облако как функцию Гаусса с двумя различными ширинами – по x и y. Однако это становится потенциальным
источником погрешности. Назовем такой метод условно «метод двумерной лавины».
Название связано с тем, что решение, из-за осевой симметрии задачи все величины
зависят от двух координат: x –
вдоль оси, и радиальной координаты r.
Избежать описанных выше проблем позволяет другой метод
расчета α. Именно, рассмотрим лавину в однородном поле между плоскими
протяженными электродами, исключив зависимость от координат, оси которых
перпендикулярных полю (рисунок 2524).
Получается, что электроны стартуют с равномерно заряженной области по всему
отрицательному электроду. Физически это трудноосуществимо, однако такая
постановка задачи не должна повлиять на коэффициент α. Ведь в начальной
фазе межэлектронные упругие столкновения пренебрежимо редки, как и
рекомбинация, таким образом, лавина определяется разгоном электрона в
однородном поле и столкновениями с нейтральными атомами. То есть электроны в
лавине ведут себя независимо. Это не выполняется лишь при
переходе в нелинейную фазу, когда объемный заряд начинает влиять на поле.
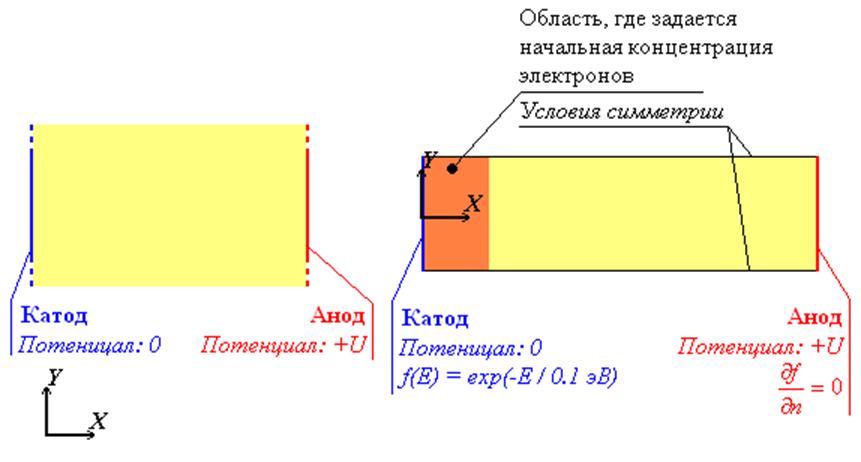
Рисунок 2524.
Постановка задачи об одномерной лавине (слева) и модель в CFD-ACE (справа).
В этой задаче, назовем ее «задачей об одномерной лавине», все величины зависят лишь от координаты x вдоль поля.
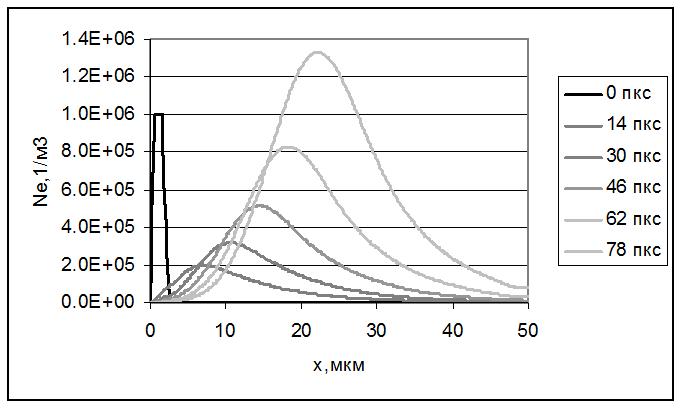
Рисунок 2625.
Концентрация электронов в «одномерной лавине» в разные моменты времени.
Решение CFD-ACE позволяет получить в виде таблицы зависимость концентрации ne от координаты x (рисунок 2625).
Поскольку формально лавина простирается бесконечно далеко по поперечным
координатам, полное число электронов N в лавине
берется в расчете на единицу площади поверхности поперечного сечения задачи. Для
подсчета N необходимо
численно взять интеграл от концентрации электронов по x от катода до анода:
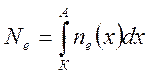
Центр лавины xc подсчитывается по формуле:
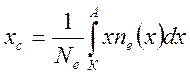
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.