Лавинный механизм в сильном электрическом поле, страница 12

Распределение электронов по энергиям (спектр) не зависит не только от координаты, но и от времени, поскольку величина внешнего однородного поля не меняется. Изменяется лишь концентрация электронов.

Рассмотрим распределение электронов по энергиям (рисунок 2423), которое, как указано выше, не меняется во времени и в пространстве. Его можно получить из файла решения CFD, функция распределения электронов по энергиям и координатам, напомню, одна из тех, которые непосредственно рассчитываются при решении системы уравнений.

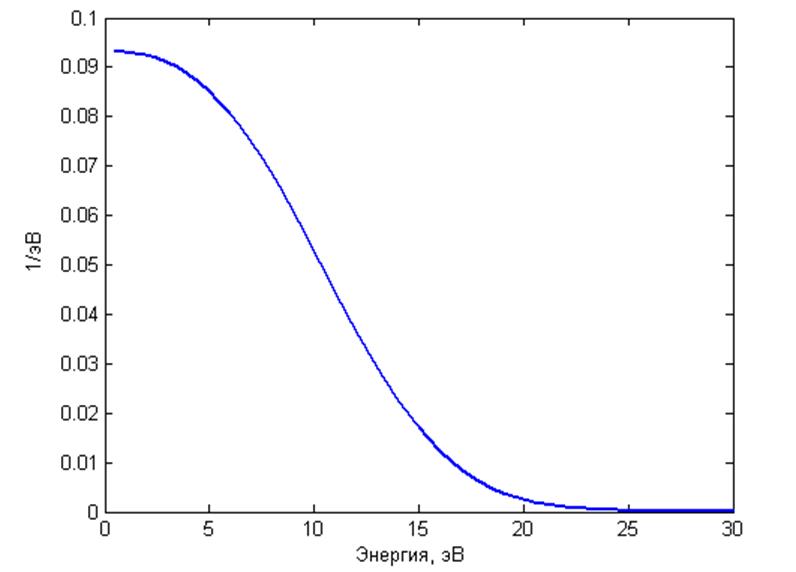
Рисунок 2423. Спектр электронов в линейной фазе лавины.

Сравнение расчета с экспериментальными данными.

Поскольку расчет начальной стадии разрядов в CFD-ACE не является общепризнанным методом, важно, что данная задача позволяет сверить результаты работы метода с экспериментальными данными для лавинных процессов в однородном поле. Простейшая модель лавины описывает одиночную лавину как дрейф облака электронов вдоль поля с диффузией. При этом полное число электронов в облаке N экспоненциально растет по мере его продвижения. Пусть x – координата центра облака. Тогда N изменяется так:

                                                                                        (2314)

По закону подобия коэффициент столкновительной ионизации α зависит от отношения E/p, где p – давление газа. Коэффициент α измеряется на опыте.

Какие эффекты определяют значение α, измеренное в эксперименте? Выше было показано, что рекомбинацию для данных процессов можно не учитывать. Коэффициент α учитывает конкуренцию возбуждения и ионизации, куда уходит энергия, набираемая электроном в электрическом поле. А это, в свою очередь, требует учета функции распределения электронов по энергиям. Наконец, поскольку исходные данные задаются в виде сечений реакций, требуется корректная оценка соотношения дрейфовой и тепловой скоростей, для перевода пробегов по реакциям в число столкновений. Таким образом, метод, правильно подсчитывающий α, должен совместно учитывать весь комплекс явлений, происходящих в лавине.

Для аппроксимации зависимости α от E/p существует полуэмпирическая формула:

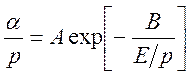                                                                                  (2415)

В справочной литературе даются коэффициенты A и B и указывается диапазон параметра E/p, в котором работает формула (2415). Например, для аргона имеем
A = 12 1/(см∙торр), B = 180 В/(см∙торр), при атмосферном давлении формула работает в диапазоне от 75 до 450 кВ/см. Численно рассчитав коэффициенты α при различных напряженностях поля, мы получаем материал для сравнения метода с опытными данными.

Итак, для определения коэффициента столкновительной ионизации α необходимо найти зависимость Ne(x), где Ne – полное число электронов в пространстве в некоторый момент времени, а x – координата центра электронного облака. Затем полученную зависимость нужно сравнить c формулой (2314).

Для определения Ne, в принципе, необходимо взять объемный интеграл от концентрации электронов, которая выводится в файл решения CFD-ACE. В силу осевой симметрии задачи, в данном случае он сводится к двумерному. Однако средствами CFD-ACE такую операцию не выполнить, а вывести данные для обработки в другой программе не удается. Возможный путь решения – определять параметры аналитической функции (2516), а затем брать от нее объемный интеграл, предполагая, что она правильно описывает ситуацию. Рассмотрим подробнее этот метод.

Электронное облако быстро теряет свою изначально цилиндрическую форму, и решение принимает вид, приблизительно описываемый функцией:

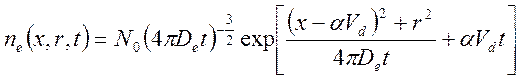                                                                                                            (2516)

Формула (2516) является приблизительной. Ее вид в пространстве в определенный момент времени описывается функцией Гаусса, а полное число электронов растет со временем следующим образом:

                                                                                (2617)