Лавинный механизм в сильном электрическом поле, страница 5

Это статистическое уравнение, в котором неизвестное – только продольная составляющая скорости V_t. Можно провести усреднение по столкновениям, вводя частоту столкновений ν (число ударов в единицу времени) и средний косинус угла отклонения – эта характеристика реакции не сильно отличается от нуля. Обычно вводят эффективную частоту столкновений: ν_эфф =ν(1-<cosθ>).

Надо сказать, что предположение о том, что частота столкновений не зависит от энергии электрона, также достаточно грубое приближение.

Получаем уравнение усредненного движения:

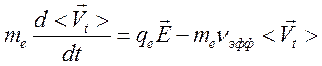                                                              (117)

Будем называть далее усредненную продольную скорость дрейфовой скоростью V_d.

Подвижность.

Уравнение (117) интегрируется для случая однородного поля. Решение имеет вид (128):

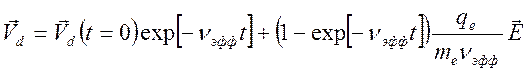                                                                                                            (128)

Решение (128) демонстрирует, что средняя продольная компонента скорости V_d быстро устанавливается. Время установления составляет порядка 1/ν_эфф, то есть порядка времени между столкновениями. Стационарное значение дрейфовой скорости V_d равно:

                                                                                           

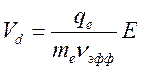
Коэффициент пропорциональности μ между дрейфовой скоростью и напряженностью поля называется подвижностью.

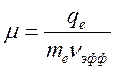                                                                                                (139)

Итак, в рамках данной модели оказывается, что электрон перемещается вдоль поля с постоянной скоростью. Но это не означает, что в среднем возникает сила, аналогичная силе трения, которая не дает увеличиваться импульсу и поглощает энергию, передаваемую электрическим полем. Ведь мы сами заложили в модель тот факт, что в упругих столкновениях энергия не теряется. Противоречия здесь нет, столкновения останавливают рост средней скорости, но не среднеквадратичной.

Дрейфовая и тепловая скорости.

Дрейфовая скорость V_d определяет перемещение электрона в пространстве на масштабах много больше пробега между столкновениями. В каких случаях можно использовать эту величину?

Плотность электрического тока при движении набора частиц с зарядами q_i и скоростями V_i в области пространства с объемом V равна:

                                                                  

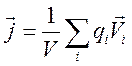
При большом числе частиц в объеме с одинаковыми зарядами происходит усреднение вектора скорости. Таким образом, с электрическим током связана именно усредненная скорость <V>, то есть дрейфовая скорость.

С другой стороны, способность электрона ионизовать или возбудить молекулу, зависит от его кинетической энергии. Средняя кинетическая энергия определяется среднеквадратичной скоростью <V²>. Назовем эту величину тепловой скоростью V_th:

                                                                  

Именно через нее выражается средняя кинетическая энергия электронов:

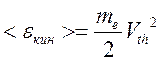                                                                                        (1410)

Полный путь и путь по дрейфу.

Дрейфовая скорость позволяет вычислять перемещение электрона за много упругих ударов. Выше было показано, что вне зависимости от начальной скорости через несколько упругих ударов электрон в среднем начинает двигаться вдоль силовой линии. Значит, на больших масштабах мы можем считать, что электрон двигается вдоль силовой линии. Силовая линия поля представляет усредненную гладкую траекторию движения электрона в воздухе. Длина участка силовой линии, которую прошел электрон, называют путь по дрейфу.

Однако реальная траектория электрона оказывается хаотичной, а значит, более протяженной. Длина реальной траектории электрона называется полный путь.

Дрейфовая скорость дает нам перемещение электрона вдоль силовой линии на больших пространственных масштабах, а значит, связана с путем по дрейфу s_d:

                                                               

Тепловая скорость связана с полным путем s_полн: