Лавинный механизм в сильном электрическом поле, страница 14

 Зависимость Ne(xc) хорошо аппроксимируется экспоненциальной функцией, как показано на рисунке 2726. Сравнивая зависимость с (2314), мы видим, что показатель экспоненты равен αxc. Отсюда по результатам аппроксимации получаем коэффициент столкновительной ионизации. Например, для случая E=80 кВ/см, показанном на рисунке 2726, зависимость Ne(xc) аппроксимируется функцией , отсюда α=0,1743 1/мкм.

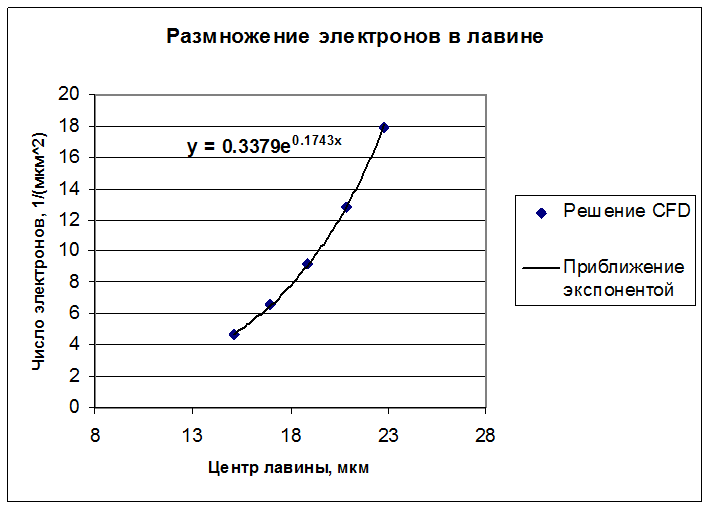
Рисунок 2726. Подсчет полного числа электронов в определенный момент времени позволяет определить коэффициент столкновительной ионизации. E = 80 кВ/см.

График на рисунке 2827 демонстрирует, насколько определенные разными методами коэффициенты α соответствуют опытным данным. Моделируя «двумерную лавину», развивающуюся из компактного пакета, мы получаем разумные результаты, однако отклонение от опытной кривой все же составляет 10-20%. По методу «одномерной лавины» отклонение уже составляет всего 2-5%.

Отклонение составляет 5% для точки 80 кВ/см, которая находится на границе применимости формулы, и 4% для 300 кВ/см. Точки, относящиеся к более слабым полям (100 кВ/см и 200 кВ/см), отклоняются от опытных данных на 1-2%. Погрешность самого метода, то есть погрешность определения коэффициента α в формуле (2314), составляет 1-2%.

Необходимо отметить, что большей точности проверки достигнуть нельзя, поскольку коэффициенты A и B в эмпирической формуле (2415), установленные по опытным данным, даны с двумя значащими цифрами.

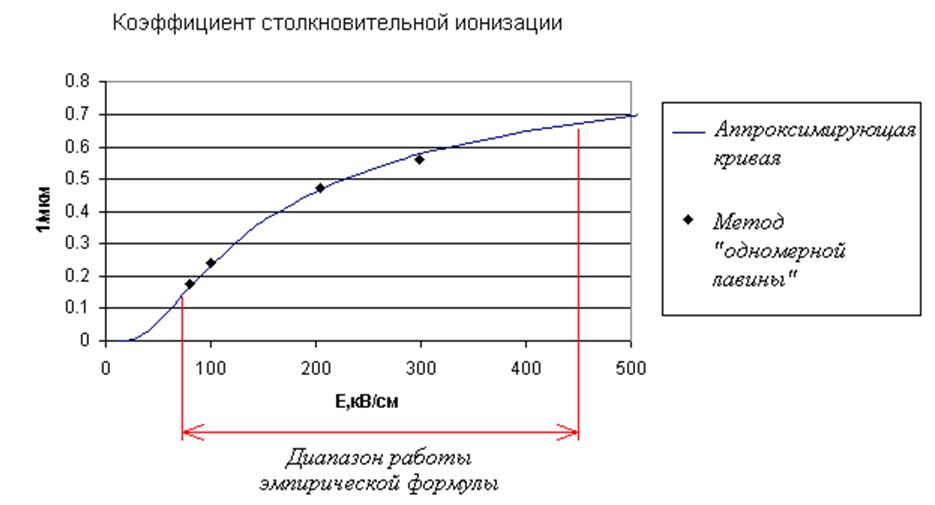 Рисунок 2827. Результаты сравнения численного решения с экспериментальными данными по коэффициенту столкновительной ионизации.

Рисунок 2827 позволяет утверждать, что описанный выше метод позволяет с хорошей точностью восстановить вид кривой зависимости коэффициента столкновительной ионизации от напряженности поля. Это подтверждает то, что решение CFD-ACE правильно описывает развитие лавины в аргоне, а, следовательно, процессы дрейфа, ионизации, возбуждения, по крайней мере в полях 80-300 кВ/см.

Измерение тока при прохождении лавины[U1] .

На опыте коэффициент α измеряют по регистрации тока в цепи, содержащий разрядный промежуток. Этот ток имеет нетривиальный характер – он не связан непосредственно с поглощением заряда на электроде. Ток идет и тогда, когда заряды еще не достигли электродов. Природа тока связана с тем, что при движении заряженной частицы в газе, на поверхности проводника происходит перераспределение зарядов, которые должны экранировать поле частицы (рисунок 2931).

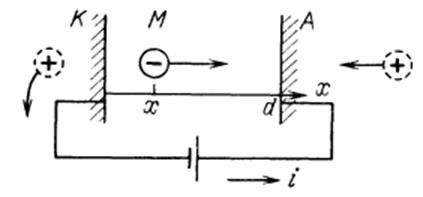
Рисунок 2931. Схема протекания тока в цепи при прохождении разряда через газовый промежуток.

Можно получить величину тока, анализируя электростатическую задачу о перераспределении поверхностных зарядов на проводнике, однако есть более короткий путь. Рассмотрим движение частицы с зарядом q в однородном поле E, имеющем только компоненту Ex. При дрейфе частицы вдоль поля на расстояние dx поле совершает над ней работу dA=qExdx. Ясно, что эта работа производится источником напряжения. Однако источник находится вне поля, он взаимодействует лишь со своим участком цепи. Поэтому совершаемая им работа равна dA=I∙Udt. Перенос энергии осуществляется через ток I,  связанный с перераспределением зарядов на электродах. Приравнивая работы, получаем:

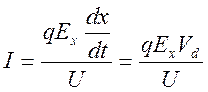                                                                                (3040)

Ясно, что работы, производимые над зарядами, суммируются, поэтому при наличии зарядов в формуле (3040) необходимо взять сумму токов, создаваемых каждым зарядом.

Отсюда мы можем сразу вывести теоретическую формулу для тока, создаваемого лавиной. Рассмотрим газ без прилипания.

При каждой ионизации возникает положительный ион и электрон, , поэтому, пока лавина не контактирует с электронами, их число равно. Поскольку поле еще не изменено объемным зарядом, все электроны поле E_x, с одинаковой скоростью V_e = μ_e∙E_xток, создаваемый ей, равен:. Аналогично, все ионы движутся со скоростью V_ion = μ_ion∙E_x:

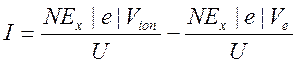                                                                (3141)