Лавинный механизм в сильном электрическом поле, страница 11

Постановка задачи.

Рассматривается следующая задача (рисунок 1615). Имеется компактный объем, заполненный электронами с концентрацией 10¹⁶ 1/м³. Эта область представляет собой цилиндр с радиусом 10 мкм и высотой 20 мкм. Таким образом, в начальный момент в ней находятся 63 электрона.

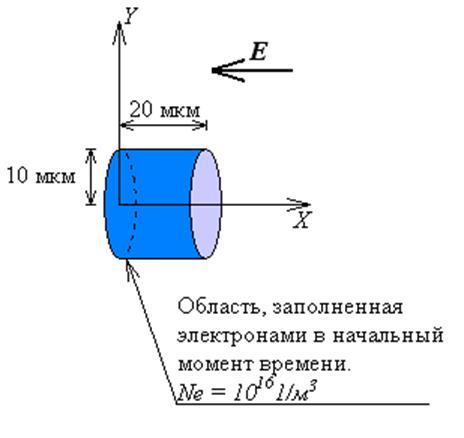
Рисунок 1615. Постановка задачи о развитии одиночной лавины в однородном поле.

Ясно, что задача обладает осевой симметрией. Можно ввести цилиндрическую систему координат с осью симметрии X, и решение не будет зависеть от угла φ. CFD-ACE позволяет использовать двумерную модель для задач с цилиндрической симметрией. Модель должна быть конечной в пространстве, поэтому необходимо задать границы и указать соответствующие граничные условия для создания однородного поля в начальный момент времени. Рисунок 1716 демонстрирует модель с граничными условиями. В данном случае была взята разность потенциалов U=2 кВ, что обеспечило напряженность однородного поля 40 кВ/см.

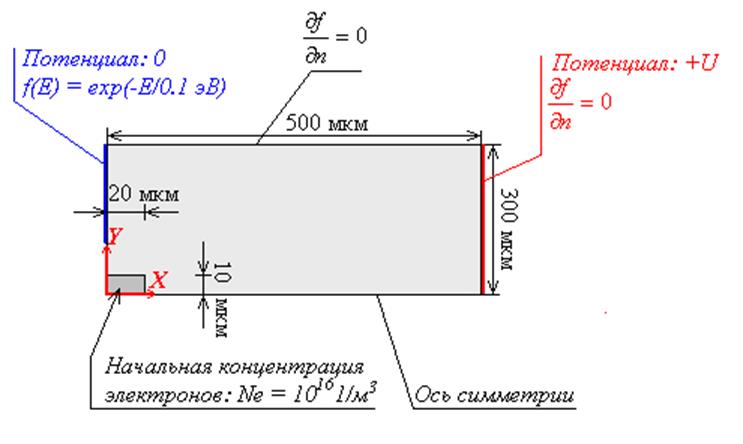
Рисунок 1716. Модель, используемая для численного расчета.

Результаты расчета.

Рассматривается задача со значением однородного поля 40 кВ/см.

Контурные графики на рисунке 1817 демонстрируют концентрацию электронов в различные моменты времени.

 

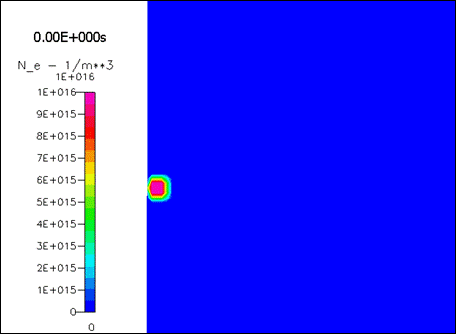
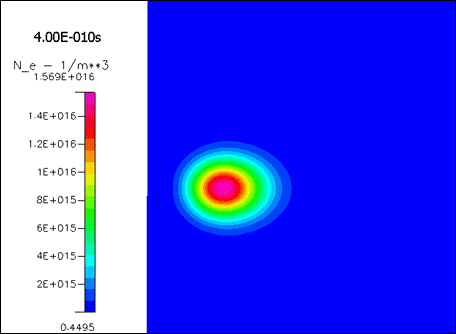
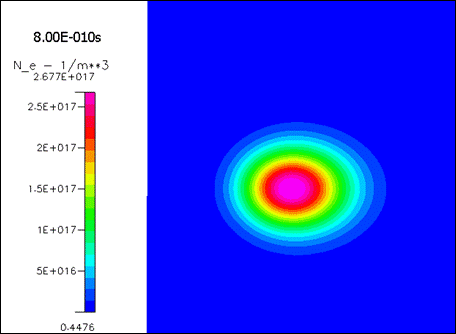
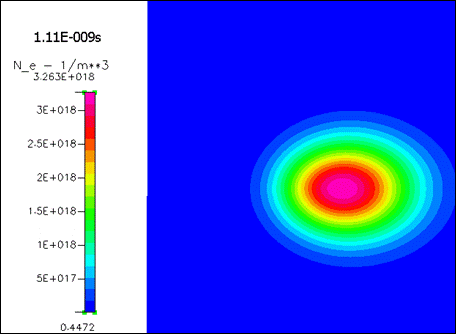
Рисунок 1817. Концентрация электронов в разные моменты времени.

Видно, что облако электронов быстро теряет свою первоначальную форму – это следствие ильной диффузии. Однако форма облака – не шарообразная, а вытянутая вдоль поля. При данном значении поля размножение происходит достаточно быстро – максимум концентрации возрастает более чем в 10 раз при перемещении всего на несколько ширин исходного пакета.

Рисунок 1918 показывает, что в первое время концентрация электронов повсеместно меньше того значения, которое было задано в исходном пакете (10¹⁶ 1/м3). Это неизбежное следствие диффузии, которая сглаживает перепады концентрации. При этом полное число электронов, конечно, не уменьшается. Затем концентрация переходит через минимум и начинается рост.

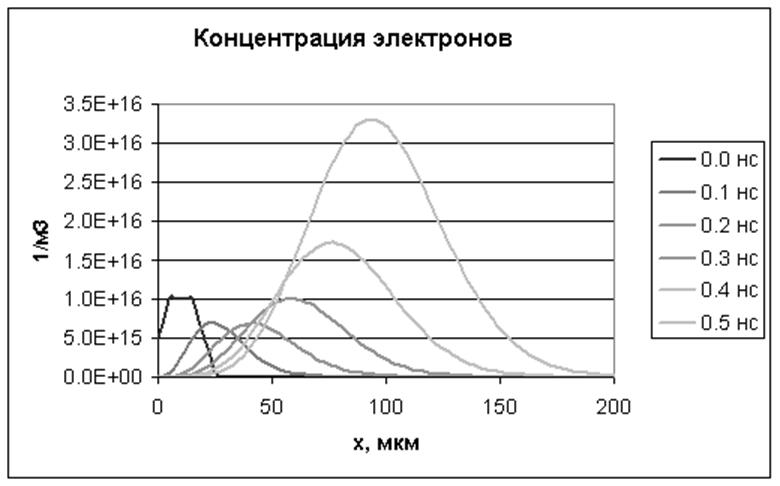
Рисунок 1918. Концентрация электронов на оси X (оси симметрии задачи) в различные моменты времени.

Рассмотрим теперь концентрацию ионов. Подвижность ионов на 3 порядка меньше подвижности электронов, поэтому они практически не двигаются  с места за время, когда электронное облако проходит расстояние, показанное на графиках. Таким образом, концентрация ионов образует своеобразный «след» лавины. На рисунке 2019 продемонстрированы контурные графики концентрации ионов в разные моменты времени.

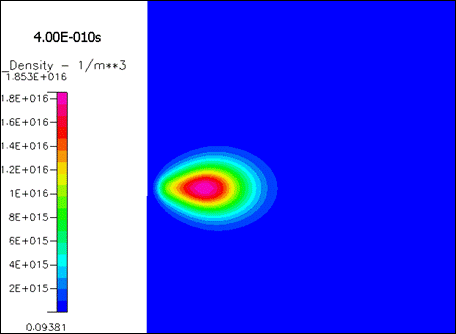
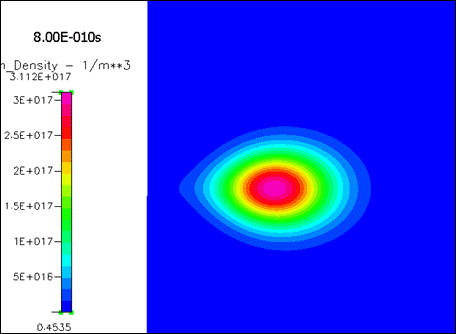
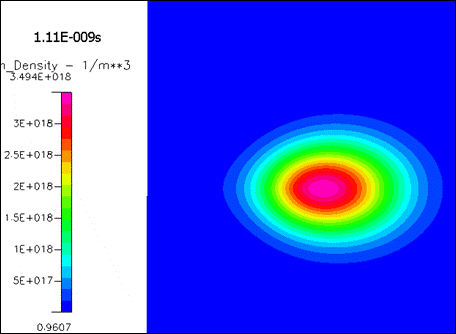
Рисунок 2019. Концентрация ионов в разные моменты времени.

Форма ионного облака в первые моменты времени имеет некоторое сходство с конусом, но затем из-за очень быстрого роста электронной концентрации «старые» ионы практически не видны на фоне огромного количества «новых», только что рожденных ионов. И форма ионного облака быстро стремится к форме электронного облака.

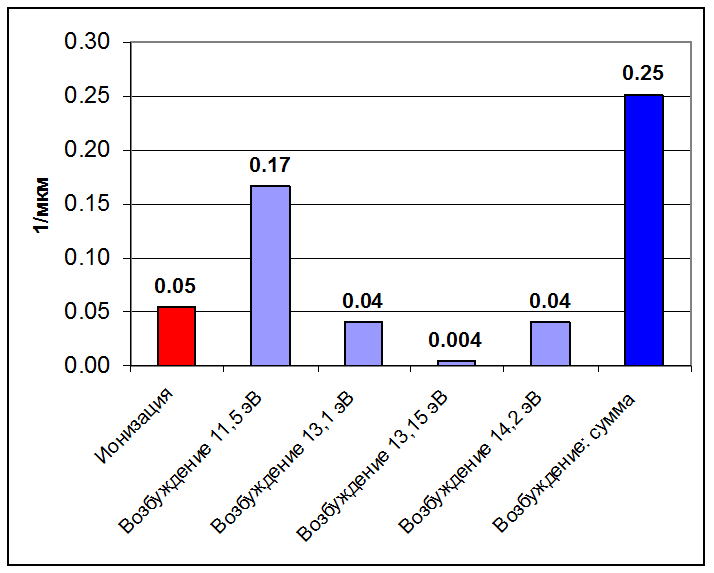
Рисунок 2120. Количество неупругих столкновений данного сорта, испытываемых одним электроном на единице пути по дрейфу. Количество упругих столкновений: 23 1/мкм.

Также решение позволяет увидеть разделение зарядов (рисунок 2221). Передняя часть лавины заряжена отрицательно, задняя – положительно, причем со временем абсолютные значения плотности растут.

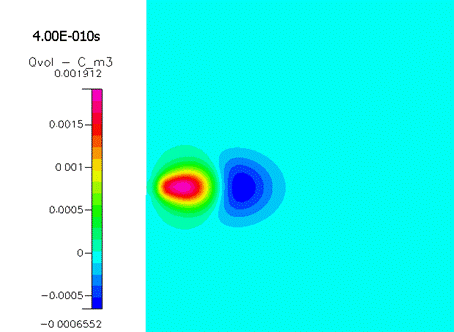
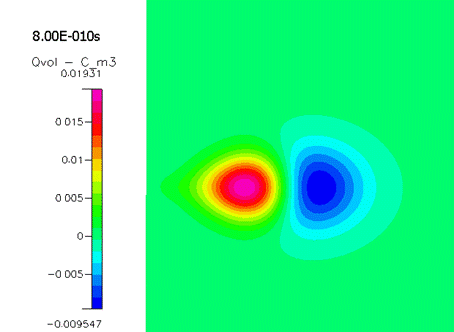
Рисунок 2221. Плотность электрического заряда в разные моменты времени.

Рисунок 2322 позволяет сравнить электронную концентрацию и их температуру.

           

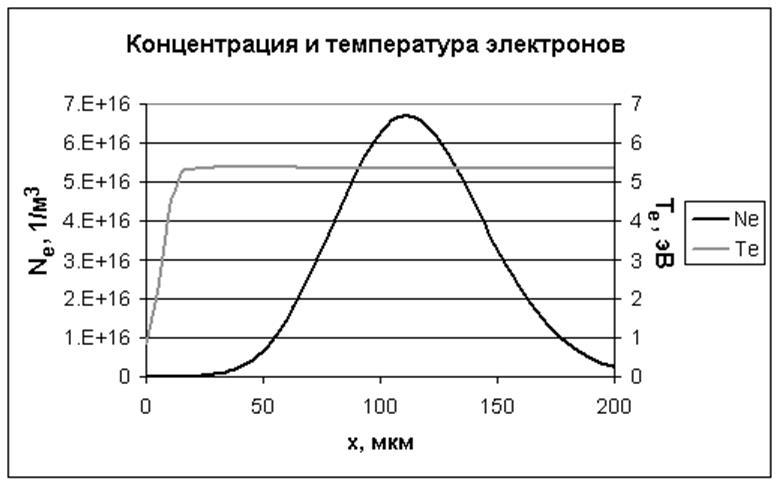
Рисунок 2322. Сравнение концентрации электронов и их температуры.
Момент времени t=0.6 нс.

Температура – так же, как и напряженность поля - распределена по лавине практически однородно. Скачок слева является следствием граничных условий – на катоде задана температура 0,1 эВ, и электрон должен пройти определенную разность потенциалов, чтобы достичь высоких энергий. Но далее энергия электронов практически неизменна – держится на уровне 5,3 эВ.