Расчет и разработка детали «вал», изучение его свойств, страница 21

В практике испытаний материалов на трение скольжения часто для реализации высоких контактных давлений используется схема сфера-плоскость. Обычно, принимая неизнашиваемым сферический образец, изучают изнашивание плоского, при этом возникает ряд сложностей, например, в определении пути трения, при оценке деформационной составляющей силы трения и т.д. Предложено перейти в этой схеме к неизнашиваемому плоскому образцу и определять характеристики изнашивания сферического образца.

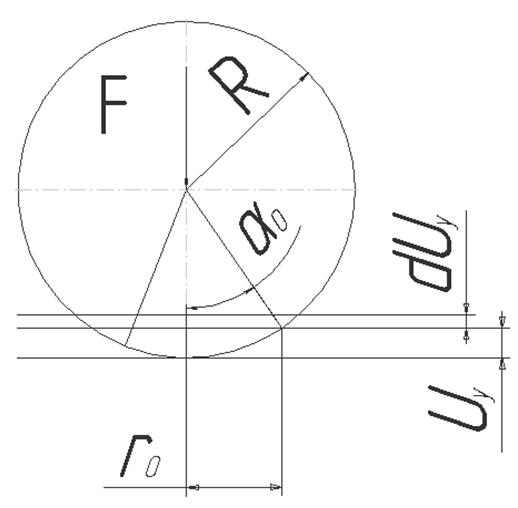
Рисунок 42. Схема контакта сферического образца (индентора) и плоского контртела.

Запишем закон интенсивности изнашивания в следующем виде:

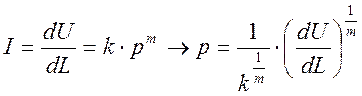      (1)

U - износ в произвольной точке поверхности трения; •

L - путь трения;

р - контактное давление;

k - коэффициент, характеризующий износостойкость материалов и условия работы данной пары;

m - показатель степени, его величина изменяется в пределах от 1 до 3 и выше в зависимости от вида износа, приработки и т.п.;

Далее запишем выражение нормальной нагрузки:

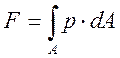          (2)

Уравнение элементарной площадки контакта выглядит следующим образом:

    (3)

Подставляя уравнения (1) и (3) в выражение (2) получим зависимость:

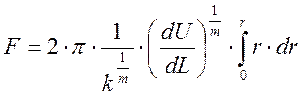;        (4)

Запишем условие касания сферического индентора и контртела:

U_y = y;

r₀ = x.

Рассмотрим два случая:

1). Когда показатель степени m = 1.

Уравнение контактного давления:

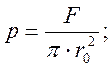                 (5)

Подставляя в формулу (5) уравнение (4) получим:

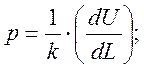            (6)

Запишем уравнение окружности:

               (7)

Раскрывая скобки получаем:

           ;          (8)

При U ‹‹ 2·R имеем:

      (9)

Приравнивая уравнения (5) и (6) и подставляя в них уравнение (9) получим:

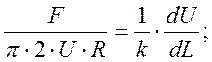             (10)

Далее решаем дифференциальное уравнение первого порядка:

            

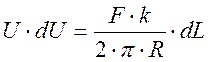
Получаем значение износа сферического индентора в том случае если U ‹‹ 2 ∙ R, т.е. уравнение окружности вырождается в уравнение параболы:

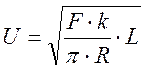                        (11)

Контактное давление равно:

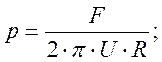                     (12)

При U ≤  2 · R.

Приравняем уравнения (5) и (6) и подставим в них уравнение (7):

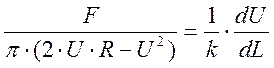  ;           (13)

Разделим переменные:

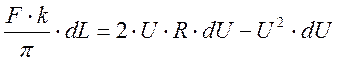;               (14)        

Упрощая выражение получим:

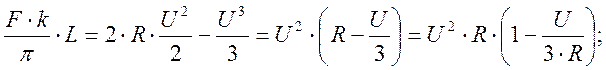
Формула для вычисления износа:

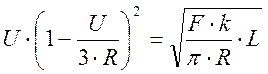
Контактное давление равно:

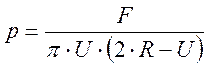
2). Рассмотрим случай когда показатель степени m≠1.

Приравняем уравнения (1) и (5):

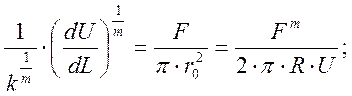
Возведём обе части уравнения в степень m:

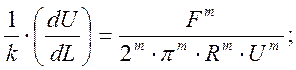
Разделим переменные и решим дифференциальное уравнение I порядка:

;

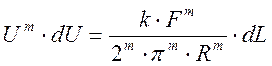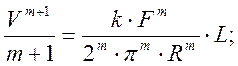
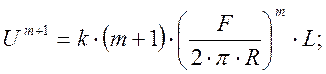
В окончательном виде получаем выражение для величины износа в общем случае:

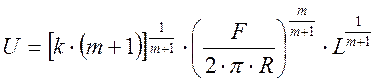;              (15)

Построим некоторые зависимости:

9.  Графики изменения величины износа при переменной нагрузке и пути трения L = 1000 м.

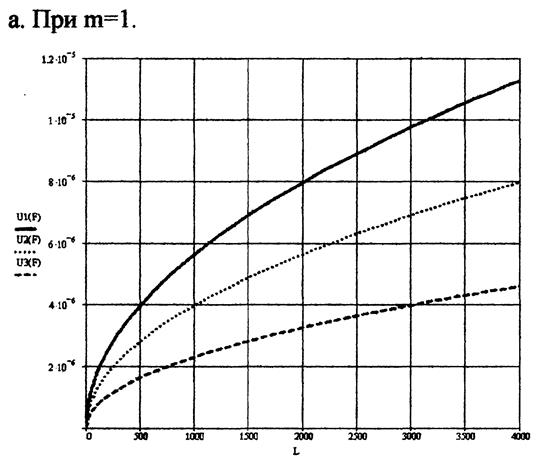
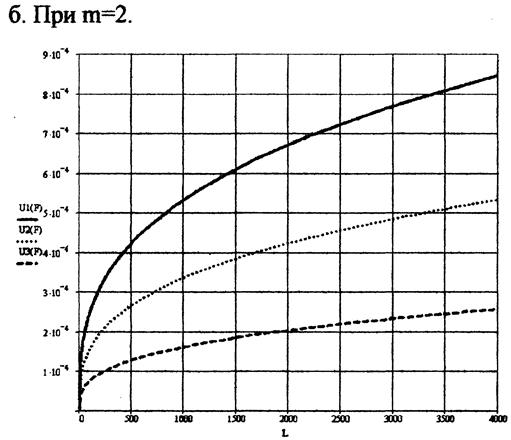
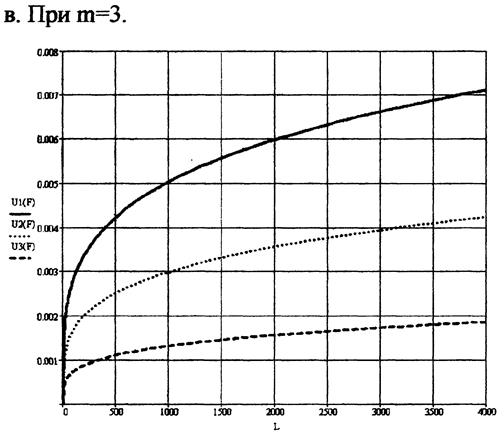
10.  График изменения величины износа при постоянной нагрузке F=10 Н:

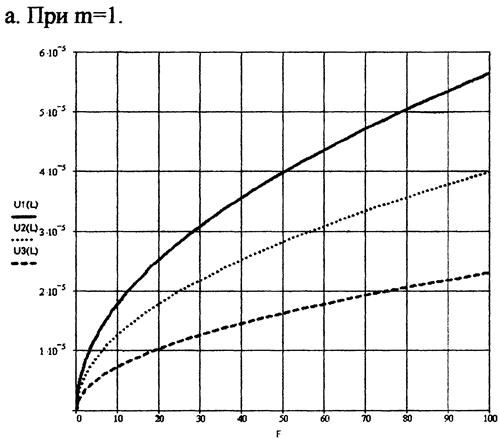
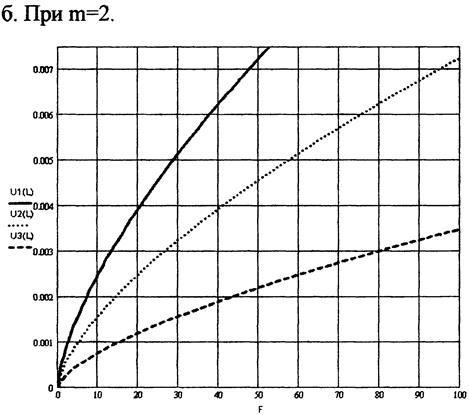
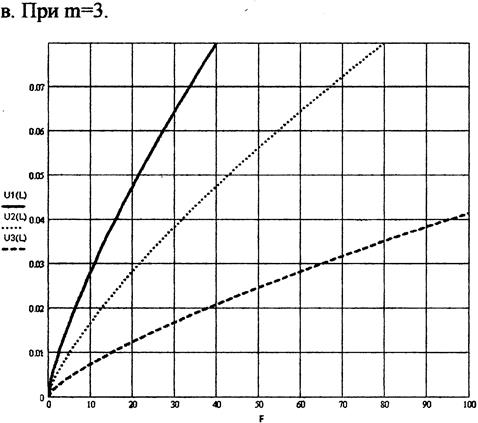
На приведённых графиках:

______ соответствует радиусу образца R=5 мм.

……… соответствует радиусу образца R=10 мм.

--------- соответствует радиусу образца R=30 мм.

2. Технологический раздел.

2.1 Материал детали «Вал» и его свойства.

Деталь «Вал» изготавливается из материала Ст40. Ст40 – углеродистая, качественная, конструкционная сталь – применяется для изготовления коленчатых валов, шатунов, маховиков – после улучшения; длинных валов (l>5d), ходовых валиков, зубчатых колес – после поверхностного упрочнения с нагревом ТВЧ (на 1-  2 мм).

Ограничено свариваемая.                                                    

Модуль упругости –  Е = 2∙10⁵  МПа

Модуль сдвига – G = 7.4·10⁴  МПа       

^{Таблица 2. Химический состав стали 40 ГОСТ 1050-88,%}

C	Si	Mn	Cr	S	P	Cu	Ni	As
0.37-0.45	0.17-0.37	0.50-0.80	Не более
			0.25	0.04	0.035	0.25	0.25	0.08

2.2.  Анализ технологичности детали «Вал».