Расчет и разработка детали «вал», изучение его свойств, страница 19

Максимальное значение относительной ширины зубчатых колёс:

                                                                                                            

 

Величину относительной ширины колёс найдём по следующей зависимости:

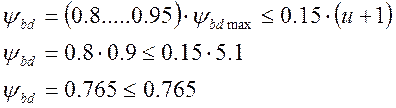
4. Расчет начальных и делительных диаметров колес 1 и 2.

Коэффициент учитывающий распределение нагрузки:

Коэффициент учитывающий динамические нагрузки:

Коэффициент учитывающий неравномерность распределения нагрузки:

Начальные диаметры для зубчатых колёс I и 2:

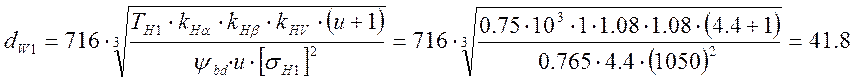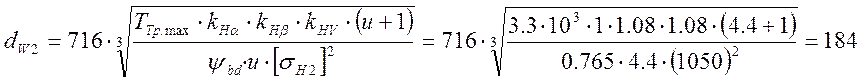мм

мм

У зубчатых передач без смещения или при суммарном смещении  x_Σ = 0 начальные и делительные диаметры колёс совпадают т.е:

d_W1 = d₁ = 41.8  мм

d_W2 = d₂ = 184  мм

5.   Расчёт числа зубьев колёс 1 и 2.

Примем модуль зубьев равным m = 2 мм.

Рассчитаем число зубьев для колёс 1 и 2:

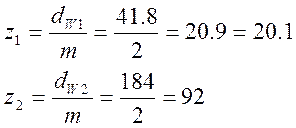
6.  Расчёт ширины венцов зубчатых колёс 1 и 2.

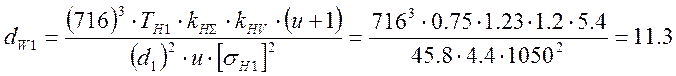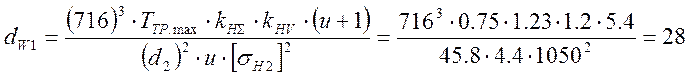 мм

 мм

7.  Расчёт на прочность активной поверхности зубьев.

В основу расчёта на прочность активной поверхности зубьев положена формула Герца, имеющая следующий вид:

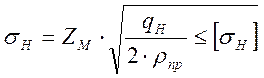
Расчётная удельная нагрузка:

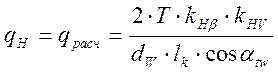
Длина контактных линий в зацеплении:

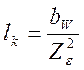
Коэффициент учитывающий коэффициент торцового перекрытия:

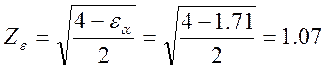
Коэффициент зависящий от механических характеристик материалов зубчатых

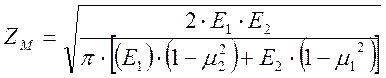   , где

Е - модуль упругости материалов колёс. Для выбранного материала колёс Е₁ = Е₂ = 2·10⁵МПа.

μ - коэффициент Пуассона. Для конструкционных материалов коэффициент

Пуассона располагается в пределах  μ = 0.25......0.35. Без существенной погрешности принимают μ₁ =μ₂= 0.3.

Подставляя значения Е и μ в формулу коэффициента Z_M получим:

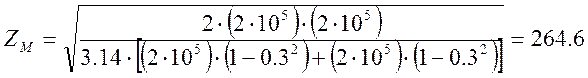
Угол зацепления α_twпримем равным 20 °.

Приведенный радиус кривизны:

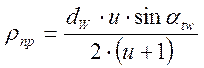
Подставляя все выше приведенные значения в формулу Герца получим:

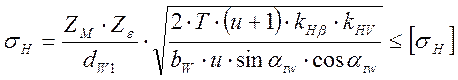
Значения расчётных контактных напряжений одинаковы для обоих колёс. Поэтому расчет выполним для большего колеса 2:

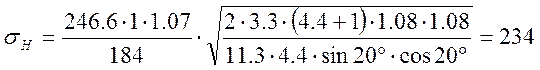МПа ≤ 1050 МПа

Следовательно условие прочности активных поверхностей зубьев выполняется.

8. Расчёт прочности зубьев по напряжениям изгиба.

Формула для нахождения величины напряжения изгиба выглядит так:

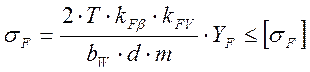
Коэффициент учитывающий неравномерность распределения нагрузки:

Коэффициент учитывающий динамические нагрузки:

Коэффициент формы зубьев определяем по графику:

Предел прочности при цементации:

  МПа

Допускаемые напряжения изгиба рассчитаем по формуле:

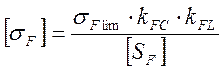  , где

k_FC - коэффициент определяемый характером приложения нагрузки к зубу.

k_FC = 1 при нереверсивной нагрузке.

k_FL - коэффициент долговечности. Примем k_FL = 1.

[S_F]  -  допускаемый коэффициент запаса прочности, примем равным [S_F] = 1.7 .

Подставляя значения приведённых выше коэффициентов в формулу допускаемых напряжений получим:

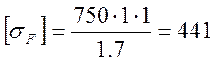 МПа

Найдём значения напряжений изгиба для колёс 1 и 2:

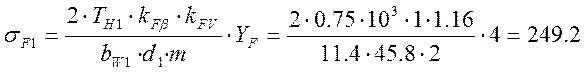 МПа ≤ 441 МПа

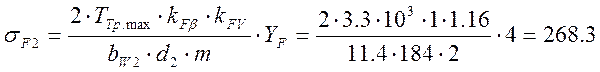 МПа ≤ 441 МПа

Следовательно условие прочности по напряжениям изгиба выполняется.

1.6.3. Расчёт корпуса, фланцев и креплений на прочность.

Все расчеты сделаны в пакете Machcad и представлены в конце пояснительной записки.

1.6.4. Расчёт криогенной системы.

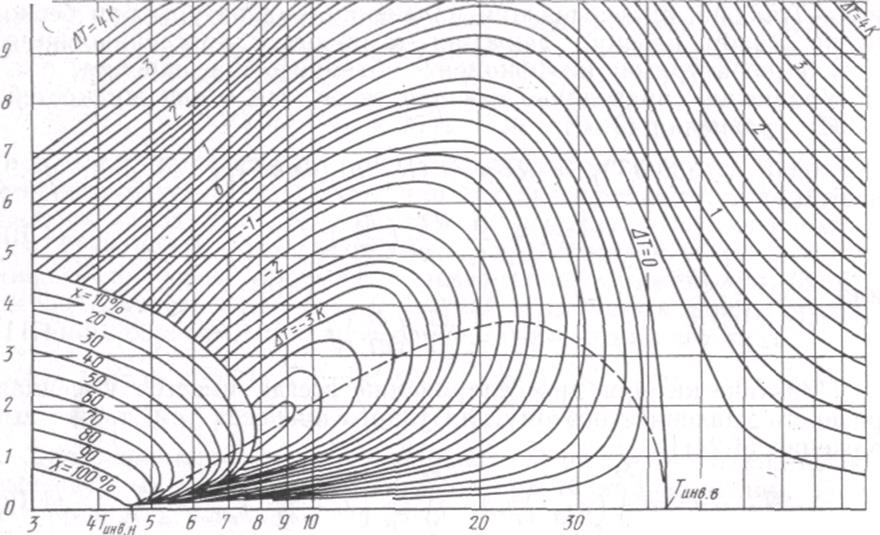
Для охлаждения разного рода аппаратуры до температур 4—8 К созданы микрокриогенные установки, основанные на различных принципах получения холода: на принципе изоэнтальпического расширения газа (дроссельные установки в нашем слечае). Дроссельные однокаскадные установки служат для получения температур порядка 35—90 К.

Определим изменение температуры гелия, находящегося при начальной температуре Т_Н=180 К и давлении p_H = 10 МПа(100 кгс/см²) при дросселирование.Конечное давление р_к = 0,1 МПа (1 кгс/см²).v=0.1 м/с ;f=1

Воспользовавшись диаграммой состояния (Т — S) для гелия, найдем, что температура гелия после дросселирования понизится на 153 К и составит 27 К.

Суммарный теплоприток от  силы трения, фланцев и вала составляет  Q=19.7 K

     Диаграмма  изменения  температуры  гелия  при дросселировании до  давления 0,1 МПа (штриховая линия — кривая инверсии; р и Т — давление и температура перед  дросселированием; х — доля жидкости после дросселиро­вания).