Разработка нелинейного радиолокатора для обнаружения электронных устройств, содержащих нелинейные компоненты, страница 37

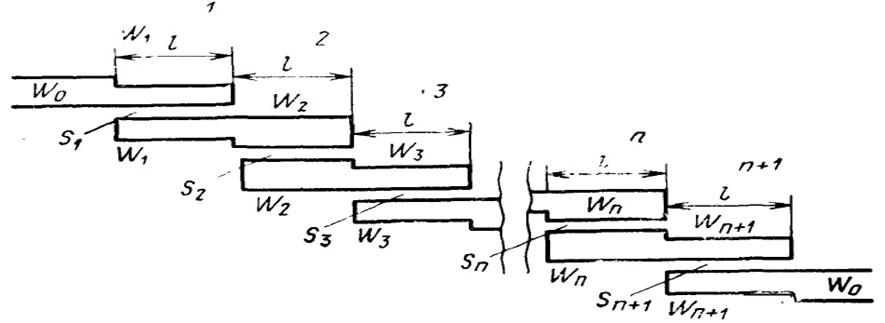
Рис. 7.1.1. Микрополосковый полосовой фильтр.

Microwave Office является мощной и удобной средой для моделирования и оптимизации различных радиоэлементов и цепей. Сначала смоделируем фильтр входной цепи канала приема второй гармоники. Результаты представлены на рисунке 7.1.2. или в приложении 2.

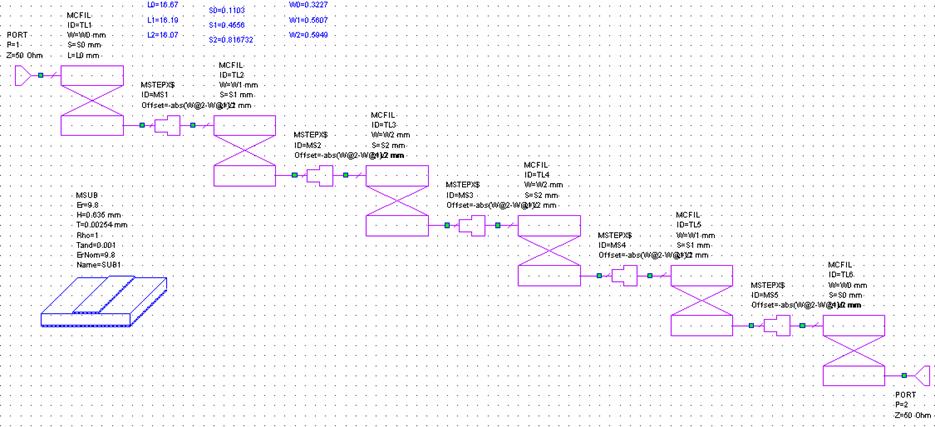
Рис 7.1.2. Схема микрополоскового фильтра 2ой гармоники (1710..1890 МГц).

При этом внешний вид фильтра и его размеры следующие:

Рис 7.1.3. Внешний вид микрополоскового фильтра 2ой гармоники.

В результате моделирования были получены следующие параметры фильтра:

 мм.          мм.   мм.

 мм.          мм.   мм.

 мм.          мм.   мм.

Видно, что размеры фильтра, полученные в результате моделирования близки к размерам, полученным в ходе теоретических расчетов.

Теперь рассмотрим характеристики промоделированного фильтра:

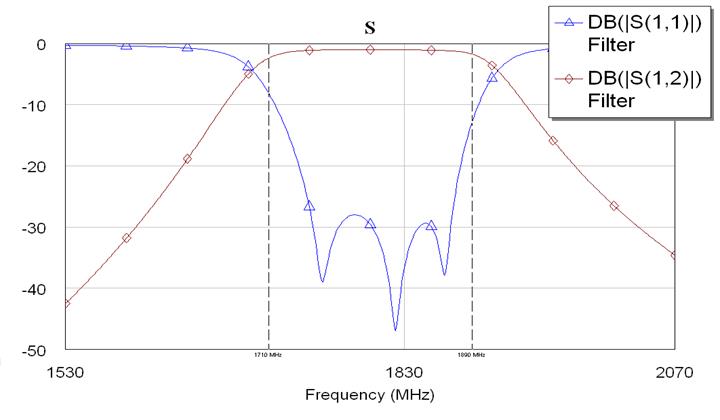
Рис. 7.1.4. S-параметры фильтра канала приема второй гармоники.

Где S(1,2) – коэффициент передачи от входа к выходу. (Классически данная характеристика обозначается S(2,1), но в Microwave Office приняты иные обозначения: Здесь первое число обозначает куда подается тестовый сигнал, а второе – где производится измерение).

S(1,1) – коэффициент отражения по входу.

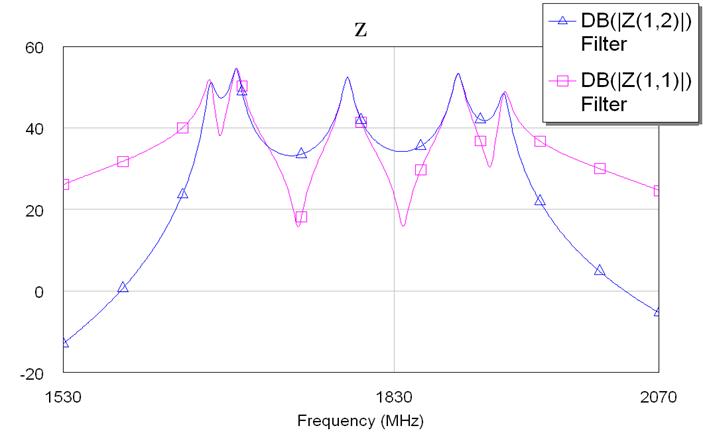
Рис. 7.1.4. Z-параметры фильтра канала приема второй гармоники.

Здесь, аналогично, Z(1,2) – проходное сопротивление.

Z(1,1) – входное сопротивление.

Как видно из приведенных графиков, в результате моделирования получился фильтр с хорошей линейностью характеристики в полосе пропускания, достаточной крутизной и подавлением вне полосы пропускания.

Microwave Office позволяет также изменять параметры смоделированных узлов и наблюдать изменения на графиках в режиме реального времени. Используя данную возможность, экспериментально было установлено, что наибольшее влияние на параметры микрополосковых фильтров оказывает изменение размера . Так, изменение c 16,1 мм до 17,78 мм приводит к существенным изменением коэффициентов S(1,1) и S(1,2), что наглядно продемонстрировано на рисунке 7.1.5:

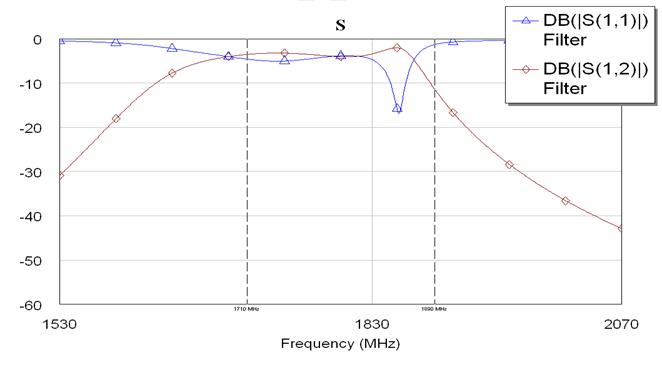
Рис. 7.1.5. Изменение S параметров фильтра канала приема второй гармоники.

Аналогичное влияние длины   имеют и на Z параметры фильтра:

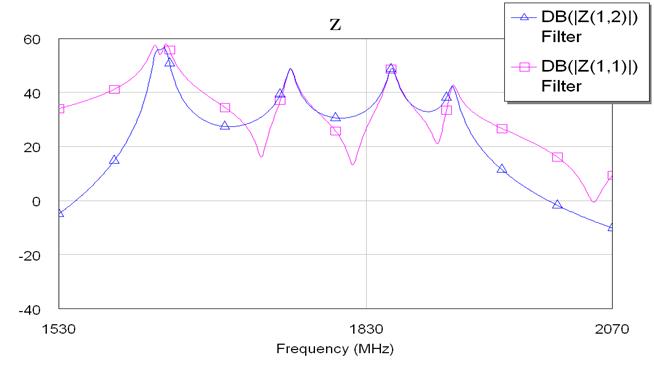
Рис. 7.1.6. Изменение Z параметров фильтра канала приема второй гармоники.

Так же, промоделируем фильтр входной цепи канала приема третьей гармоники.

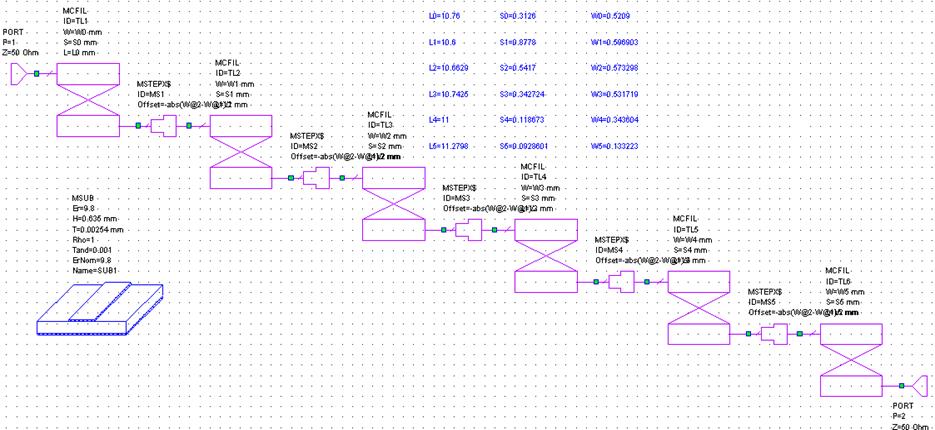
Рис. 7.1.7. Схема микрополосковго полосового фильтра канала приема третьей гармоники.

Рис. 7.1.8. Внешний вид полосового фильтра канала приема третьей гармоники.

В результате моделирования получены следующие параметры фильтра:

 мм.      мм.   мм.

 мм.      мм.   мм.

 мм.  мм.   мм.

 мм.  мм.   мм.

 мм .          мм.   мм.

 мм.  мм.     мм.

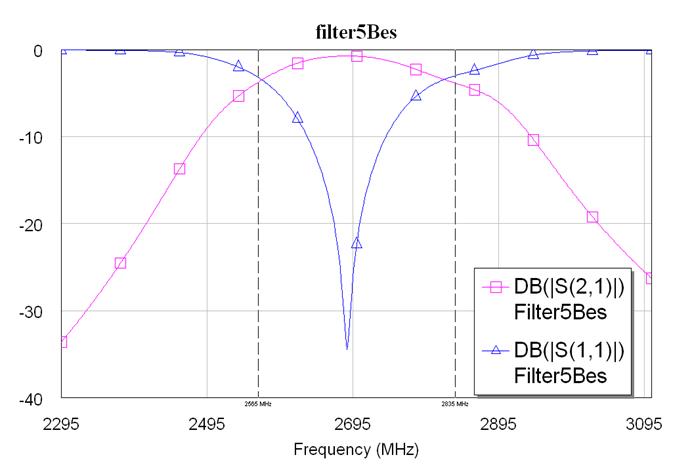
Рис. 7.1.9. S параметры фильтра канала приема третьей гармоники.

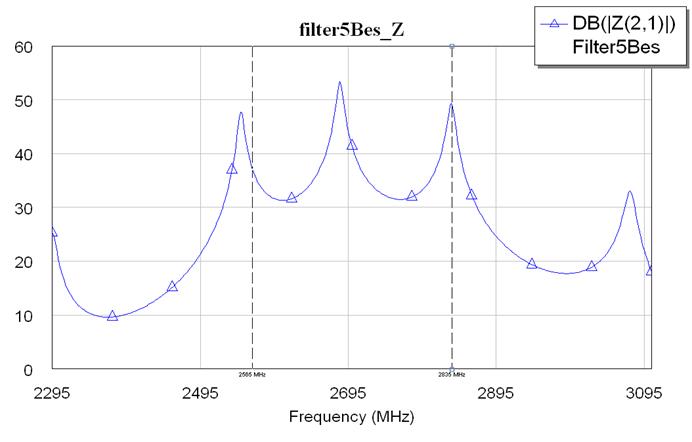
Рис. 7.1.10. Z параметры фильтра канала приема третьей гармоники.

Для того, что бы удостовериться, что именно параметр  оказывает наибольшее влияние на характеристики фильтра повторим эксперимент с данным фильтром.

Изменения  и  по прежнему оказывает незначительное влияние на характеристики фильтры, а изменение  с 10,7602 мм до 11,8362 мм вновь приводит к существенным изменениям:

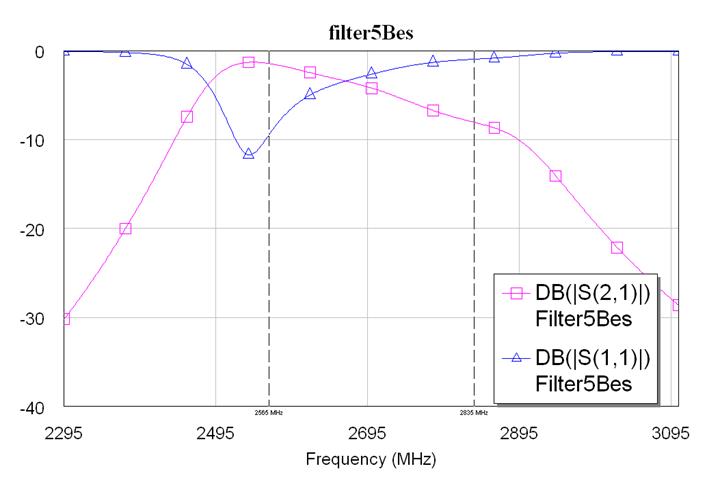
Рис. 7.1.11. Изменение S параметров фильтра канала приема третьей гармоники.

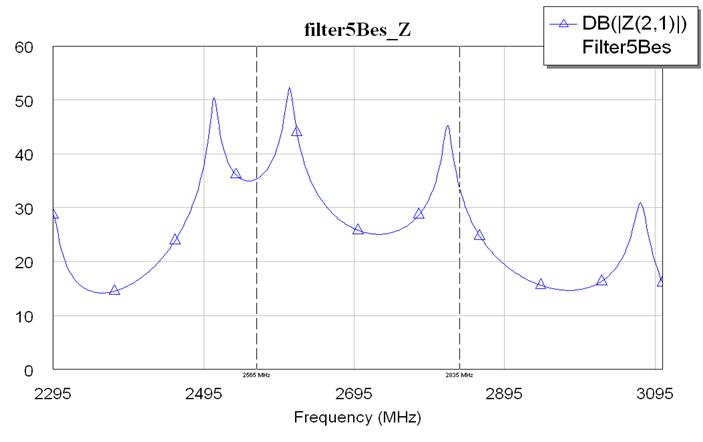
Рис. 7.1.12. Изменение Z параметров фильтра канала приема третьей гармоники.

Можно сделать вывод, что именно размеры  являются наиболее критичными при производстве микрополосковых фильтров, используемых в проектируемом устройстве. Погрешности в 1 мм (~10%) вносят существенные изменения в характеристики фильтра. По этому необходимо как можно точно выдерживать при производстве заданные размеры микрополосковых линий и не допускать погрешности более ±5%.

7.2.Моделирование работы нелинейного радиолокатора.

Как отмечалось в теоретической части, работа нелинейного радиолокатора основана на сравнении уровней мощности второй и третьей гармоники принятого сигнала. Для искусственной нелинейности (например транзистор или диод) уровень второй гармоники обычно не менее чем на 20 дБ выше, чем третьей. Для естественной нелинейности, напротив, уровень третьей гармоники оказывается выше уровня второй.