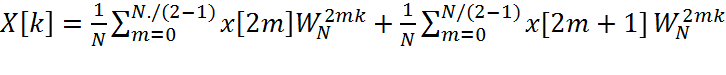Разработка нелинейного радиолокатора для обнаружения электронных устройств, содержащих нелинейные компоненты, страница 21

 (2.9.1.2)

Но так как 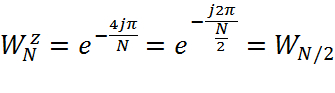 то
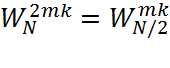 . Следовательно, (2.9.1.2) можно записать в виде

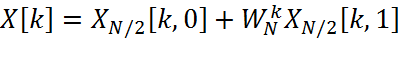, (2.9.1.3)

где каждое из слагаемых является преобразованием длины N/2

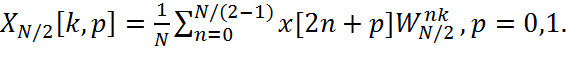 (2.9.1.4)

Заметим, что последовательность (WN/2)^nk периодична по k с периодом N/2. Поэтому, хотя номер k в выражении (2.9.1.3) принимает значения от 0 до N-1, каждая из сумм вычисляется для значений k от 0 до N/2-1. Можно оценить число комплексных операций умножения и сложения, необходимых для вычисления преобразования Фурье в соответствии с алгоритмом (2.9.1.3). Два N/2-точечных преобразования Фурье по формулам (2.9.1.4) предполагают выполнение 2(N/2)² умножений и приблизительно столько же сложений. Объединение двух N/2-точечных преобразований по формуле (2.9.1.3) требует еще N умножений и N сложений. Следовательно, для вычисления преобразования Фурье для всех N значений k необходимо произвести по N+N²/2 умножений и сложений. В то же время прямое вычисление по формуле (2.9.1.1) требует по N² умножений и сложений. Уже при N>2 выполняется неравенство N+N²/2 < N² , и, таким образом, вычисления по алгоритму (2.9.1.3)-(2.9.1.4) требуют меньшего числа математических операций по сравнению с прямым вычислением преобразования Фурье по формуле (2.9.1.1). Так как вычисление N-точечного преобразования Фурье через два N/2-точечных приводит к экономии вычислительных операций, то каждое из N/2-точечных ДПФ следует вычислять путем сведения их к N/4-точечным преобразованиям:

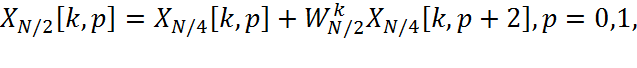  (2.9.1.5)
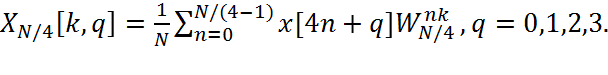    (2.9.1.6)

При этом, вследствие периодичности последовательности W^nk_N/4 по k с периодом N/4, суммы (2.9.1.6) необходимо вычислять только для значений k от 0 до N/4-1. Поэтому расчет последовательности X[k] по формулам (2.9.1.3), (2.9.1.5) и (2.9.1.6) требует, как нетрудно подсчитать, уже по 2N+N²/4 операций умножения и сложения.
 Следуя таким путем, объем вычислений X[k] можно все более и более уменьшать. После m=log₂N разложений приходим к двухточечным преобразованиям Фурье вида

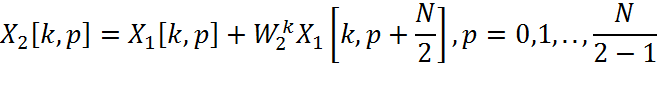
где "одноточечные преобразования" X₁[k,p] представляют собой просто отсчеты сигнала x[n]:

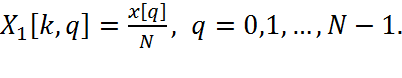
 В итоге можно записать алгоритм БПФ, получивший по понятным причинам название алгоритма с прореживанием по времени :

X₂[k,p] = (x[p] + W^k₂x[p+N/2]) / N,

где k=0,1, p=0,1,...,N/2 -1;

X_2N/M[k,p] =X_N/M[k,p] + W^k_2N/MX_N/M[k,p+M/2],

где k=0,1,...,2N/M -1, p=0,1,...,M/2 -1;

..X[k] = X_N[k] =X_N/2[k,0] + W^k_NX_N/2[k,1],

где k=0,1,...,N-1

 На каждом этапе вычислений производится по N комплексных умножений и сложений. А так как число разложений исходной последовательности на подпоследовательности половинной длины равно log₂N, то полное число операций умножения-сложения в алгоритме БПФ равно Nlog₂N. При больших N имеет место существенная экономия вычислительных операций по сравнению с прямым вычислением ДПФ. Например, при N = 2¹⁰ = 1024 число операций уменьшается в 117 раз.
 Рассмотренный нами алгоритм БПФ с прореживанием по времени основан на вычислении преобразования Фурье путем формирования подпоследовательностей входной последовательности x[n]. Однако можно использовать также разложение на подпоследовательности преобразования Фурье X[k]. Алгоритм БПФ, основанный на этой процедуре, носит название алгоритма с прореживанием по частоте[26].

2.9.2. Случайные процессы и спектральная плотность мощности.

Дискретный случайный процесс x[n,i] можно рассматривать как некоторую совокупность, или ансамбль, действительных или комплексных дискретных временных (или пространственных) последовательностей, каждую из которых можно было бы наблюдать как результат проведения некоторого эксперимента (n - временной индекс, i - номер наблюдения). Последовательность, полученную в результате одного из наблюдений будем обозначать x[n]. Операцию усреднения по ансамблю (т.е. статистического усреднения) будем обозначать посредством оператора <>. Таким образом, <x[n]> - среднее значение случайного процесса x[n] в момент времени n. Автокорреляция случайного процесса в два различных момента времени n1 и n2 определяется выражением r_xx[n₁,n₂]=<x[n₁]x*[n₂]>.